Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 24

A viga é sustentada por um pino em e por um cabo de ancoragem de aço . Se o cabo tiver diâmetro de , determine o carregamento w se a extremidade for deslocada para baixo.

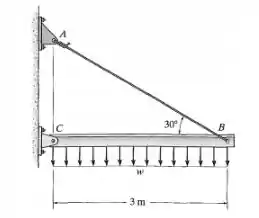
Passo 1

Primeiramente, devemos multiplicar a carga w pela distância de 3m para acharmos a força resultante da carga distribuída. Ela ficará no meio da viga. Agora, vamos colocar nossa força Fab na direção do cabo. Fazendo o DLC, ficaria assim:

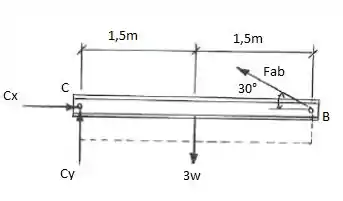
Aplicando-se as equações de equilíbrio, podemos achar Fab:

Vamos agora desenhar o estado deformado:

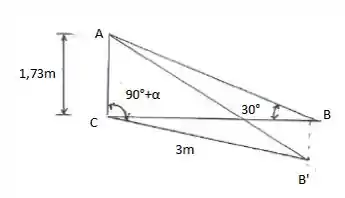
Sabemos que o lado AB vale:

Como a deformação é dada (18mm), podemos calcular o valor de pela relação:

Passo 2

Com isso, podemos calcular, por lei dos cossenos, o valor de AB’:

Agora, com o valor do comprimento final, podemos calcular a deformação:

-3

Como temos o módulo de elasticidade do aço A-36, que vale 200MPa, podemos ter a relação entre a deformação e a tensão:

-3

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de nylon esta submetido a uma tração de 10 N. sabendo que E = 3,2G P a , que a máxima tensão de tração admissível é de 40 MPa e que o comprimento do fio não pode ser incrementado em mais do que

Uma barra de latão amarelo quadrada não deve se alongar mais de 1,4 mm quando submetida a uma força de tração. Sabendo que E = 70G P a e que a resistência à tração admissível é120 MPa, determine (a) o

A barra BD feita de aço (E = 200G P a ) é utilizada para contenção lateral da haste comprimida ABC. O máximo esforço que se desenvolve em BD é igual a 0,02P. Se a tensão não deve exceder 124,1 MPa e a

O cabo BC de 4 mm de diâmetro é feito de um aço com E = 200G P a . Sabendo que a máxima tensão no cabo não pode exceder 190 MPa e que a deformação do cabo não deve exceder 6 mm, determine a máxima for

Um tubo de alumínio com 250 mm de comprimento (E = 70G P a ) , 36 mm de diâmetro externo de 28 mm de diâmetro interno pode ser fechado em ambas as extremidades por meio de tampas com rosca simples de