Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 24
O cabo passa sobre a pequena polia ideal sem uma alteração em sua tensão. Qual comprimento de cabo é necessário para equilíbrio estático na posição mostrada? Qual é a tensão no cabo ?
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede duas coisas:
i) Determinar o comprimento que o cabo deve ter para que o sistema esteja em equilíbrio;
ii) Determinar a tensão do cabo devido ao peso de do cilindro.
Show de bola! Vamos começar então isolando o cilindro e analisando o diagrama de corpo livre dele.
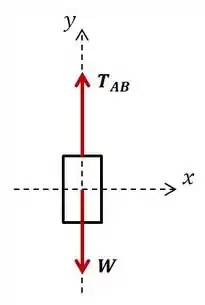
Fazendo o somatório de forças em relação a , temos:
Passo 2
Beleza! Feito isso, vamos isolar a polia , nela estão atuando três tensões: duas do cabo (já conhecida) e uma de . Novamente vamos utilizar as equações de equilíbrio para tentar descobrir .
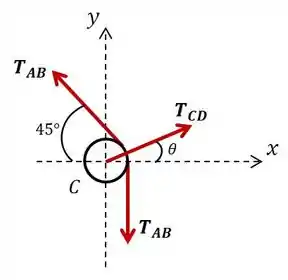
Em temos:
E em :
Relacionando e :
Passo 3
Tá, mas e agora??
Uma vez que já temos e , podemos voltar nas equações de equilíbrio em torno de ou de , isolar e calcular o seu valor.
Passo 4
Beleza, agora só falta calcularmos o comprimento do cabo . Para isso, vamos usar o esquema abaixo:
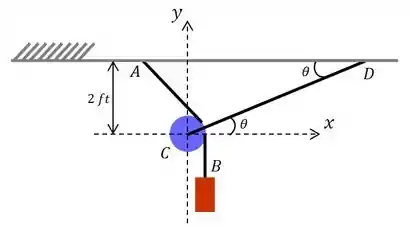
Assim fica mais fácil visualizar né? é dado por:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 