Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 102
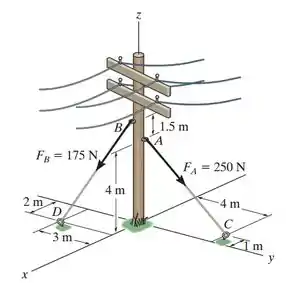
Os cabos de tração são usados para suportar o poste telefônico. Represente a força em cada cabo na forma de um vetor cartesiano. Despreze o diâmetro do poste.
Passo 1
Falaaa! Então, uma forma de expressar uma força na forma cartesiana como ele pede é achar um vetor unitário na direção e sentido e da força, e multiplicar o nosso módulo da força por esse vetor. É isso que vamos fazer aqui. Vem!
Para expressar nossas forças como vetor vamos começar encontrando as coordenadas dos pontos que definem a sua direção.
Percebe que está na direção e sentido que sai de e vai para . Já saí de e vai para . Vamos reunir as coordenadas desses pontos:
Definimos agora nossos vetores posição (os que estão na direção e sentido da força) pelo ponto final menos inicial:
Como está na direção e sentido que sai de e vai para , fazemos:
Já para :
Passo 2
Agora encontramos o módulo dos nossos vetores:
E então o vetor unitário que determina a direção e o sentido dos nossos vetores das forças vão ser aqueles vetores do passo anterior divididos pelo módulos deles, aí achamos vetores unitários:
Passo 3
Com isso, podemos expressar nossas forças como vetores cartesianos: