Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 11.Problemas fundamentais - Ex. 3

O mecanismo está sujeito a uma força P = 2 kN. Determine o ângulo θ para o equilíbrio. A mola está livre quando θ = 0 ° . Despreze a massa dos membros.

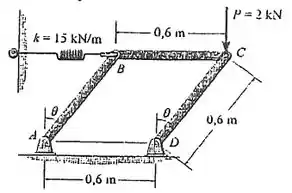
Passo 1

Vamos começar fazendo um diagrama de forças ativas, as forças que podem vir a gerar um trabalho virtual:

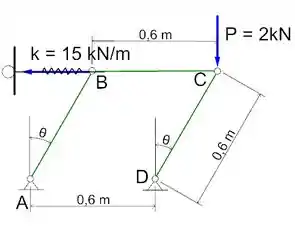
Passo 2

Sabemos pelo Princípio do Trabalho Virtual que o somatório do trabalho das nossas forças ativas é nulo:

δ U = U B + δ U C = 0

F e δ x + P δ y = 0

O deslocamento que o trabalho virtual da mola causaria é:

x = 0,6 sin ⁡ θ

Enquanto que o deslocamento causado pela força P é:

y = 0,6 ⋅ cos ⁡ θ

Passo 3

Agora precisamos derivar isso em função de θ , ficamos com:

x = 0,6 sin ⁡ θ

δ x = 0,6 cos ⁡ θ δ θ

E para a segunda equação:

y = 0,6 ⋅ cos ⁡ θ

δ y = - 0,6 sin ⁡ θ   δ θ

Passo 4

Para encontrar a força da mola usamos k = 15 kN/m:

F = k s

F = k 0,6 sin ⁡ θ - 0,6 sin ⁡ 0 ° = 15 ⋅ 10 3 ⋅ 0,6 ⋅ sin ⁡ θ - 0 = 9,0 ⋅ 10 3 sin ⁡ θ

Finalmente podemos substituir nossas informações no somatório do trabalho virtual, sabendo que a força P = 2 kN:

δ U = 0  

F e δ x + P δ y = 0

( 9,0 k sin ⁡ θ ) ( 0,6 cos ⁡ θ δ θ ) + ( 2 k ) ( - 0,6 sin ⁡ θ   δ θ ) = 0

Como δ θ ≠ 0 :

9,0 k sin ⁡ θ 0,6 cos ⁡ θ - ( 2 k ) ( 0,6 sin ⁡ θ   ) = 0

cos ⁡ θ = 2 9,0

θ = cos - 1 ⁡ 2 9,0

θ = 77,16 °

Resposta

θ = 77,16 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a intensidade exigida da força P para manter o equilíbrio do mecanismo em θ = 60 ° . Cada membro tem uma massa de 20 kg.
A ponte de 2 Mg, com centro de massa no ponto G, é levantada pelas duas vigas CD, localizadas em cada lado da ponte. Se o contrapeso E de 2 Mg estiver conectado às vigas como mostrado, determine o âng
O mecanismo conectado por pinos é restringido por um pino em A e um rolete em B. Determine a força P que deve ser aplicada ao rolete para manter o mecanismo em equilíbrio quando θ = 30 º º. A mola est
5. Determine o ângulo θ onde a barra de 50k g está em equilíbrio. A mola está livre em θ = 60 ° .
4. O mecanismo está sujeito a uma força P = 6k N . Determine o ângulo θ para o equilíbrio. A mola está livre em θ = 60 ° . Despreze a massa dos membros.