Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 52
Determine o ângulo o qual irá maximizar o momento da força de ao redor do eixo em . Calcule também o momento .
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
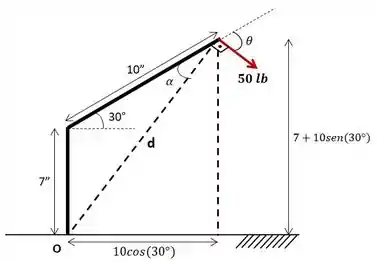
Pra começar precisamos entender o que o problema pede. Para que seja o maior possível, a força de deve agir perpendicularmente à distância que liga o ponto ao ponto de aplicação da força, que determina o maior braço de momento possível. Podemos simplificar nosso diagrama de corpo livre da seguinte forma:
Passo 2
Para determinar o ângulo precisamos primeiro encontrar o ângulo formado entre a barra de 10” e . Para isso, podemos utilizar a Lei dos Cossenos.
Se a gente considerar a extensão da barra de 10”, a soma de todos os ângulos que a compõem deve ser 180°. Como sabemos que a força de faz um ângulo de 90° com , e usando o ângulo calculado acima, temos tudo que é necessário para calcular :
Passo 3
Com isso, uma vez que já temos a distância perpendicular à força de , que liga o seu ponto de aplicação ao ponto , fica fácil determinar o momento :
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 