Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 119
A linha de força é amarrada do braço do pólo de força em A ao ponto B no mesmo plano horizontal. Por causa da curvatura do cabo no plano vertical, o cabo faz um ângulo de 15° com a horizontal onde se conecta a A. Se a tensão do cabo em A for , escreva T como um vetor e determine a magnitude de sua projeção no plano -.
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede duas coisas:
i) Expressar a tensão T (força atuante em A) como um vetor;
ii) Determinar a magnitude (módulo) da projeção de T no plano-.
Ok! Então bora começar. Neste caso, pra gente definir o vetor , precisamos determinar as suas três componentes.
Vamos começar pela componente mais simples então. Note que o vetor forma um ângulo de com o plano - apontando para baixo, sentido negativo de . Então:
Para as componentes e , vamos analisar a projeção de no plano - que é dada por:
Para decompor nos eixos -, precisamos ainda do ângulo formado pelas retas e :
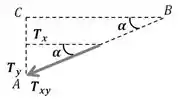
Show! Com isso, fica fácil encontrar as componentes em e :
Componente :
Componente :
Finalmente, nosso vetor é dado por:
Passo 2
Show, feito isso, uma vez que já temos o vetor , determinar sua projeção no plano - ficou bem simples. Basta a gente analisar o módulo das componentes e :
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 