Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 14

Determine a área e o centroide (overset(-)(x) , overset(-)(y)) da área.

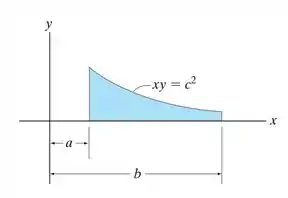
Passo 1

Faaala! Queremos a área dessa região e seu centroide. Uma coisa bem importante que a gente precisa para montar nossas fórmulinhas, antes de tudo, é definir um retângulo bem fininho dentro da nossa área, que a gente chama de elemento diferencial e encontrar a área dele.

Podemos fazê-lo paralelo ao eixo y , logo ele terá espessura d x , assim:

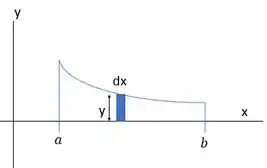
Vemos que essa área é dada por:

d A = y ⅆ x

Precisamos colocar esse y em função de x (pois temos d x ). Mas lembra que essa curvinha é

x y = c^2 -> y = (c^2)/(x)

Aí d A fica:

d A = (c^2)/(x) d x

Agora a gente precisa só de mais uma coisa. Precisamos das coordenadas do centroide desse retangulozinho. Ele vai estar no centro do retângulo, assim:

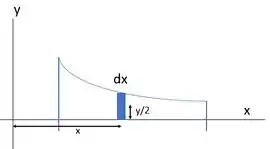
Para o centroide do nosso elemento diferencial, em overset(-)(x) temos o próprio overset(-)(x) = x , enquanto que para overset(-)(y) teremos:

overset(-)(y) = (y)/(2) = (c^2)/(2 x)

Lembra que é importante colocar tudo em função de x , porque estamos usando d x .

Passo 2

Vamos agora encontrar nossa área. A gente soma todos os retangulozinhos no intervalo de x onde nossa região está x in [ a , b ] , montando uma integral

A = int_A ⅆ A

A = int_a^b (c^2)/(2 x) d x =

A = c^2 ln x (​|_a^b

A = c^2 ln b - ln a

A = c^2 ln (b)/(a)

Passo 3

E agora encontramos nosso centroide, para overset(-)(x) temos essa fórmulinha:

overset(-)(x) = (int_A overset(-)(x) ⅆ A)/(int_A ⅆ A)

overset(-)(x) = (int_a^b x ((c^2)/(x)) ⅆ x)/(c^2 ln (b)/(a)) = (int_a^b c^2 ⅆ x)/(c^2 ln (b)/(a)) = (c^2 (x|_a^b)/(c^2 ln (b)/(a)) = (b - a)/(ln (b)/(a))

Enquanto que para overset(-)(y) :

overset(-)(y) = (int_A overset(-)(y) ⅆ A)/(int_A ⅆ A)

overset(-)(y) = (int_a^b ((c^2)/(2 x)) ((c^2)/(x) ⅆ x))/(c^2 ln (b)/(a)) = (int_a^b (c^4)/(2 x^2) ⅆ x)/(c^2 ln (b)/(a)) = (- ((c^4)/(2 x)|_a^b)/(c^2 ln (b)/(a)) = (- (c^2)/(2 b) + (c^2)/(2 a))/(ln (b)/(a)) = (c^2 (b - a))/(2 a b ln (b)/(a))

Resposta

A = c^2 ln (b)/(a)

overset(-)(x) = (b - a)/(ln (b)/(a))

overset(-)(y) = (c^2 (b - a))/(2 a b ln (b)/(a))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um arame homogêneo e fino é dobrado na forma do perímetro a seguir. Calcule o seu centro de gravidade.
Determine o centroide da área plana das figuras mostradas a seguir.
Determine o centro de gravidade da chapa metálica conformada tal como mostra a figura.
Determine o valor do ângulo θ para que a estrutura esteja em equilíbrio:
Mostre que na medida em que r 1 se aproxima de r 2 a localização do centroide o aproxima de um arco circular de raio r 1 + r 2 2 .