Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 28

Determine a componente da projeção da força ao longo da linha .

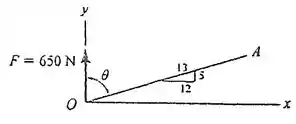
Passo 1

Como queremos a componente da projeção precisaremos da relação entre o vetor força e a linha , para isso faremos através dos seus vetores unitários.

Vamos começar encontrando o vetor unitário , usaremos a relação de catetos e hipotenusa já que a informação nos é dada através de um triângulo, assim:

Já o vetor unitário de é bem simples por estar no eixo :

Passo 2

Sabemos que , encontramos seu módulo na direção fazendo seu produto escalar com o vetor unitário , ficando:

Fazendo o produto termo a termo:

Agora que já temos seu módulo, basta multiplicar pelo vetor unitário que descobrimos as componentes da projeção da força.

(Sim, parece que você está multiplicando duas vezes, mas na primeira você obtém um escalar e depois um vetor).

Vamos lá:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a intensidade e os ângulos de direção coordenados de F 2 , de modo que a resultante das duas forças atue ao longo do eixo x positivo e tenha uma intensidade de 500 N.

O eixo S exerce três componentes de força sobre a ferramenta D . Encontre a intensidade e os ângulos de direção coordenados da força resultante. A força F 2 atua dentro do octante mostrado.

Se α = 120 ° ,β90 ° ,γ = 60° e F = 400N , determine a intensidade e os ângulos de direção coordenados da força resultante que atua sobre o gancho.

Determine a intensidade e os ângulos de direção coordenados de F 2 , de modo que a resultante das duas forças seja zero.

O poste está submetido à força F , que tem componentes atuando ao longo dos eixo x , y , z , como mostra a figura. Se a intensidade de F é 3 kN, β = 30 ° e γ = 75 ° , determine as intensidades de suas