Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 155
Para a viga e o carregamento mostrados na figura, determine a constante da mola para a qual a força da mola é igual a um terço da força total na viga.
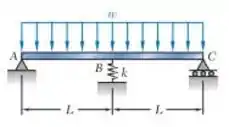
Passo 1
Fala aí, galera. Beleza? Vamos praticar mais mecânica pra tirar aquele na prova.
Esse exercício nos pede para determinarmos constante da mola. Primeiro, vamos encontrar as reações nos apoios. Para isso, vamos utilizar as equações de equilíbrio, por simetria, temos:
E também, pela lei de Hooke, vamos determinar a força elástica. Temos:
Portanto:
Agora, vamos esboçar o diagrama :
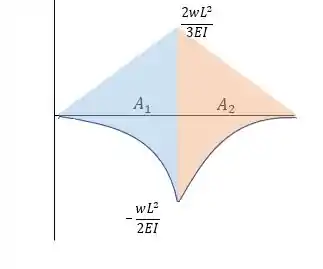
Com isso, vamos calcular cada área do diagrama . Dividimos ele em duas partes, logo:
Passo 2
Em seguida, selecionamos a tangente em como tangente de referência. Portanto:
Assim, pela Lei de Hooke:
Isolando :
É isso, galera. Bora praticamar mais!!