Os coeficientes de atrito estático e cinético entre o bloco de e o plano inclinado são e , respectivamente. Determine a força de atrito atuando no bloco quando é aplicado com uma magnitude de ao bloco em repouso, a força necessária para iniciar o movimento subindo a inclinação a partir do repouso, e a força de atrito agindo no bloco se .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar três coisas: a força de atrito para no bloco em repouso, o valor de para o bloco entrar em movimento subindo a partir do repouso e a força de atrito para .
Então bora resolver! Vamos começar analisando o diagrama de corpo livre para o item . Para facilitar nossos cálculos, vamos considerar os eixos e inclinados em acompanhando a inclinação da superfície de apoio.
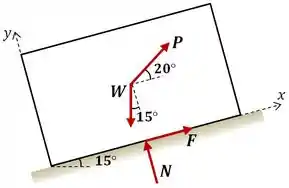
Onde:
E os coeficientes de atrito:
Passo 2
Neste caso , assumimos a condição de que a estrutura está em equilíbrio/repouso e podemos utilizar as equações de equilíbrio de forças nas direções e para determinar a reação normal de contato e a força de atrito exercidas pela superfície horizontal no bloco.
Além disso, para essa condição de equilíbrio temos que:
Uma vez que:
Nossa hipótese é válida, o corpo está em equilíbrio com (a caixa não entra em movimento).
Passo 3
Tranquilinho né? Agora vamos para o nosso segundo round! Hahaha
Começando pelo diagrama de corpo livre para a situação :
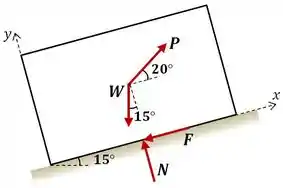
Para encontrar o valor mínimo de necessário para o bloco entrar em movimento subindo a partir do repouso, vamos considerar a situação limite, ou seja:
Com isso, fazendo o equilíbrio de forças na direção , temos:
Vamos guardar essa equação por enquanto. Já para o eixo , temos:
Substituindo na equação anterior:
Passo 4
Ainda tem coisa pra fazer?

Calma que tá acabando! Hahaha
Show de bola! Agora para o item , temos que e precisamos determinar a força de atrito neste caso. No item encontramos a força mínima necessária para que o bloco entre em movimento. Como , concluímos que o corpo está em movimento e a força de atrito cinética é dada por:
Logo, precisamos determinar a reação normal da superfície no bloco. Para isso, vamos utilizar o equilíbrio de forças na direção :
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" ![]()