Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 07
Determine o coeficiente mínimo de atrito estático que permitirá que o tambor com cubo interno fixo seja enrolado na inclinação de a uma velocidade constante sem escorregar. Quais são os valores correspondentes da força e da força de atrito ?
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o valor mínimo do coeficiente de atrito estático necessário para enrolar o tambor a uma inclinação de com velocidade constante sem que ocorra deslizamento. Pede ainda para determinar a força e a força de atrito para essa condição.
Então bora resolver! Vamos começar analisando o diagrama de corpo livre da estrutura. Para facilitar nossos cálculos, vamos considerar os eixos e inclinados em acompanhando a inclinação da superfície de apoio.
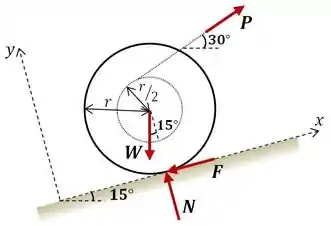
Onde:
Sabemos que o corpo está enrolando sem escorregar com velocidade constante, então:
Pela condição de equilíbrio do corpo, podemos usar o somatório de forças na direção para colocar em função das outras variáveis.
Logo:
Passo 2
Tranquilo né? Fazendo o mesmo para a direção , temos:
Passo 3
Conseguimos definir em função das outras variáveis, mas ainda temos duas incógnitas na nossa equação: e . Para a situação em que o corpo rola de escorregar com velocidade constante, a velocidade no ponto de contato do tubo com a superfície inclinada é considerada nula. Podemos então usar o equilíbrio de momentos em torno desse ponto de contato para encontrar , já que e não produzem momento em torno desse ponto, restando apenas de incógnita.
Passo 4
Calma que tá acabando hein? Hahaha Substituindo esse valor de na equação de do Passo 2, temos:
Apesar do tanto de conta até que foi tranquilo né?
Passo 5
Agora que já temos , vamos utilizar novamente o equilíbrio de forças na direção para determinar a força de atrito que foi pedida:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 