Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 44a

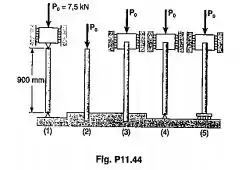
Cada uma das cinco colunas mostradas consiste de uma barra maciça de aço. Pede-se(a) sabendo-se que a coluna da Fig(1) tem 20mm de diâmetro, determinar o coeficiente de segurança em relação a flambagem para o comprimento mostrado;(b) determinar o diâmetro em cada uma das outras estruturas, para que o coeficiente de segurança seja o mesmo que o coeficiente de segurança obtido na parte a. Usar E=200GPa.

Passo 1

E aí, vamos analisar umas estruturas?

Esse exercício traz pra gente o conceito de coeficiente de flambagem e ele vai entrar no comprimento efetivo do peso crítico:

L e = K . L

E o peso crítico alterado fica:

P C R = π 2 E I L e 2 = π 2 E I K L 2

Temos 4 estruturas, mas no primeiro momento vamos analisar somente a primeira a qual temos o diâmetro, pois o item a. nos pede apenas o coeficiente de segurança e é o que acharemos. lembrando que:

F S = P C R P A D M

E agora a gente só precisa analisar que tipo de coeficiente de flambagem tem a estrutura, pra isso vamos dar uma boa olhada na figura da coluna 1.

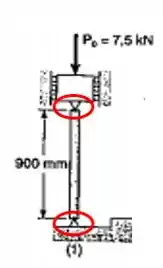
Circulado em vermelho está a vinculação da coluna, repare que se encaixa no tipo bi-rotulada então possui coeficiente de flambagem K = 1,0 .

Passo 2

Bom, como mostrado pro fator de segurança a gente precisa do momento de inércia que para seção circular é dado por:

I = π d 4 64 = π × 20 4 64 = 7,854 × 10 3 m m 4

Com tudo podemos substituir os valores na equação do peso crítico:

P C R = π 2 E I K L 2 = π × 200 × 7,854 × 10 3 1 × 900 2

E então:

P C R = 19,14 k N

E como o peso na coluna:

P C = 7,5 k N = P A D M

Temos pelo fator de segurança:

F S = P C R P A D M = 19,14 7,5 = 2,55

Resposta

a F S = 2,55

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

10.22 Uma barra de alumínio quadrada de 25,4mm de lado é mantida na posição mostrada na figura por um apoio articulado em A e por conjuntos de roletes em B e C que impedem a rotação da barra no plano
10.20 Os elementos AB e CD são barras de aço com 30mm de diâmetro, e os elementos BC e AD são barras de aço com 22mm de diâmetro. Quando o tensor é acionado, o elemento diagonal AC é colocado sob traç
10.18 Um elemento de compressão com 8,2m de comprimento de flambagem é obtido ligando-se dois perfis U de aço U200 x 17,1 com barras de travejamento conforme mostra a figura. Sabendo que o coeficiente
A barra uniforme AB de latão tem seção transversal retangular e é suportada por pinos e suportes conforme mostrado. Cada extremidade da barra pode rotacionar livremente em relação ao eixo horizontal a
10.23 A escora quadrada de 1 in. Em alumínio é mantida na posição mostrada por um pino de suporte em A e por um conjunto de roletes em B e C de modo a impedir a rotação da escora no plano da figura. S