Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 85
Cada um dos dois discos semicirculares possui uma massa de g e está soldado à haste apoiada nos mancias e , como mostrado. Calcule as forças aplicadas à haste pelo mancais para uma velocidade angular constante . Depreeze as forças de equilíbrio estático.
Passo 1
Os discos D e C estão rotacionando, então eles possuiem uma velocidade angular em torno do eixo Z.
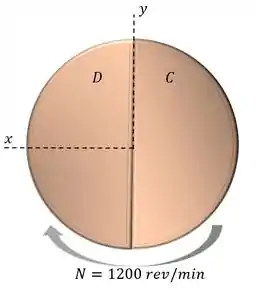
E elaborando o DCL do sistemas podemos aplicar as equações necessárias para determinar as reações nos mancais
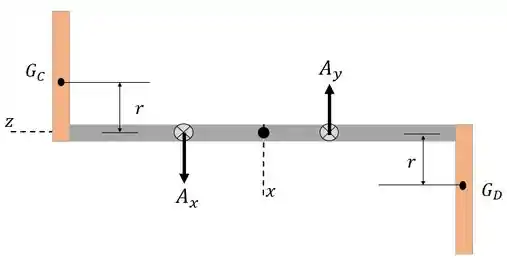
Passo 2
Então pode aplicar as equações de somatórios de momentos e forças,
E os momentos de inercia de acordo a cada plano de movimento.
Resposta
As forças nos mancais são de mesmo modulo e diferente sentidos devido a posições opostas das massas e .
Exercícios de Livros Relacionados
A placa possui uma massa de 3 kg e está soldada ao eixo vertical fixo, que gira na velocidade angular constante de 20 π r a d s . Calcule o momento M aplicado ao eixo pela placa devido ao desbalanceam
Se o mecanismo do Prob. 7/87 gira com uma velocidade angular constante maior do que a especificada na resposta para aquele problema, determine o momento de atrito M f que os pinos da articulação devem
Cada perna de 200 mm das barras de ângulo reto que estão soldados à hastte vertical possui uma massa de 0.12 kg. Calcule o momento fletor M na haste em O devido à rotação do conjunto em torno da haste
Coloque o seu livro sobre sua mesa, com eixos fixos orientados como indicado. Gire o livro em torno do eixo x através de um ângulo 90º e, em seguida, a partir dessa nova posição gire-o 90º em torno do
O robô do Prob. 7/17 é apresentado novamente aqui, onde o sistema de coordenadas x - y - z com origem em O 2 gira em torno do eixo X na velocidade angular θ ˙ . Os eixos sem rotação X - Y - Z orientad