Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 236
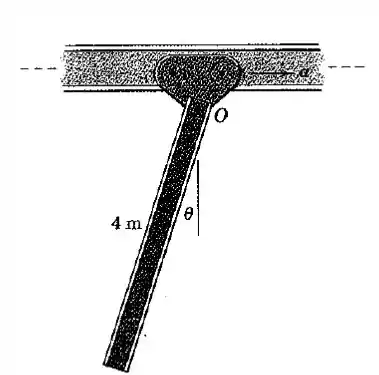
A viga I de aço deve ser transportada pelo carrinho suspenso ao qual está articulada em 0. Se o carrinho parte do repouso com e recebe uma aceleração horizontal constante α = 2m/s², encontre os valores máximos de e . O módulo da oscilação inicial poderia constituir um fator para segurança em uma oficina.
Passo 1
Definir a equação de momento:
Passo 2
Resolver equação:
Para teremos R = e resolvendo obtém-se
Passo 3
Agora considerando máximo e :
Substituindo e g obteremos o valor
Resposta
Assim θ = 11,52° , e :
Exercícios de Livros Relacionados
A roda de 10k g tem um diâmetro de 400m m e um raio de giração em relação ao seu eixo de 180m m . A roda carrega um eixo com 4k g , de pequeno diâmetro, através do seu centro como mostrado. Se a roda
Uma barra esbelta uniforme de massa M e comprimento L está em translação sobre o plano horizontal liso x - y com uma velocidade de v M quando uma partícula de massa m , que se desloca com uma velocida
Determine a quantidade de movimento angular da Terra em relação ao centro do Sol. Suponha a Terra homogênea e uma órbita circular da Terra com raio 149,6 10 6k m ; consulte a Tabela D/2 para outras in
A barra esbelta de massa m e comprimento b é articulada na sua extremidade inferior em O , na forma mostrada no detalhe separado do suporte O . A barra é liberada a partir do repouso na posição vertic
O fenômeno de “tropeço” de um veículo é investigado aqui. O veículo utilitário esportivo está deslizando para o lado com velocidade v 1 e sem velocidade angular quando atinge um pequeno meio-fio. Assu