Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 91

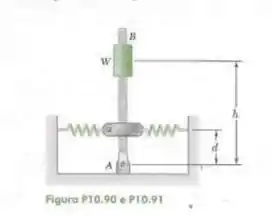
A haste AB está presa a uma articulação em A e a duas molas, cada qual de constante k. Se h = 1125 mm, k= 1kN/m e W = 270 N, determine ao menor distância d para qual o equilíbrio da haste é estável na posição mostrada na figura. Cada mola pode atuar tanto sob tração quanto sob compressão.

Passo 1

Fala aí galera, vamos para mais um problema de estática. Primeiro, temos que encontrar a energia potencial:

V = 2 1 2 k c + W y n V = k d 2 sin 2 ⁡ θ + W h cos ⁡ θ

Então, temos que:

d V d θ = 2 k d 2 sin ⁡ θ cos ⁡ θ - W h sin ⁡ θ d 2 V d θ 2 = 2 k d 2 cos ⁡ 2 θ - W h cos ⁡ θ

Passo 2

Portanto, temos equilíbrio na posição θ = 0 :

d 2 V d θ 2 = 2 k d 2 - W h

Por fim, o equilíbrio é estávem em:

d 2 V d θ 2 > 0 ,         2 k d 2 - W h > 0

2 k d 2 > W h

Substituindo os valores dados no enunciado:

2 × 1000 × d 2 > 270 × 1,125 d > 389   m m  

Resposta

d > 389   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

35- A energia potencial de um sistema mecânico é dada por V = 6 x 3 - 9 x 2 + 7 , onde x é a coordenada de posição associada ao único grau de liberdade. Determine a posição, ou as posições, de equilíb
37- A barra de massa m com centro de massa em G gira ao redor de um eixo horizontal passando por O . Verifique as condições de estabilidade para as duas posições de equilíbrio.
36- A barra uniforme de massa m e comprimento L é sustentada no plano vertical por duas molas idênticas com rigidez k é comprimidas de um comprimento δ na posição vertical, θ = 0 . Determine a rigidez
38- O pequeno cilindro de massa m e raio r está confinado a rolar sobre a superfície circular de raio R . Usando os métodos desta seção, prove que o cilindro é instável no caso a ) e estável no caso b
O cilindro está apoiado em A , vértice de um furo cônico em sua base. Determine a distância míni m a ⁡ d a fim de que ele permaneça em equilibrio estável.