Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 92
Duas barras estão presas a uma única mola de constante k que está indeformada quando as barras estão na vertical. Determine o intervalo de valores de P para os quais o equilíbrio do sistema é estável na posição mostrada na figura.
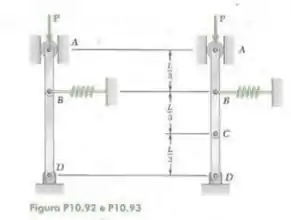
Passo 1
Fala aí galera, vamos para mais um problema de estática. Primeiro, temos que encontrar a energia potencial:
Então, temos que:
Passo 2
Portanto, temos equilíbrio na posição :
Por fim, o equilíbrio é estávem em:
Resposta
Exercícios de Livros Relacionados
45- Um dos requisitos críticos no projeto de uma perna artificial é prevenir que a junta do joelho flambe sob carga quando a perna está esticada. Como uma primeira aproximação, simule a perna artifici
42- A figura mostra a seção transversal de um basculante de ventilação de 60k g , articulado em O ao longo de sua borda horizontal superior. O basculante é controlado pelo cabo acionado por uma mola,
46- A alavanca está presa a uma das engrenagens montadas sobre mancais fixos, que estão ligadas por uma mola. A mola de rigidez k liga dois pinos, montados nas faces das engrenagens. Quando a alavanca
47- A seção transversal de um basculante articulado em relação ao eixo horizontal O , de massa m e com centro de massa em G , está mostrada na figura. A medida que o basculante abre, a mola é comprimi
48- Determine a altura máxima h da massa m para a qual o pêndulo invertido será estável na posição vertical mostrada. Cada uma das molas tem rigidez k e elas estão igualmente pré-comprimidas nessa pos