Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 44
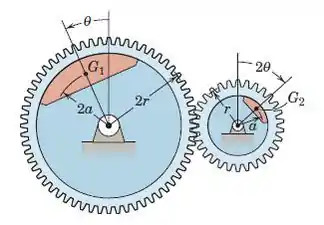
Cada uma das duas engrenagens carrega uma massa excêntrica me está livre para girar no plano vertical em torno de seu rolamento. Determine os valores de θ para o equilíbrio e identifique o tipo de equilíbrio para cada posição.
Passo 1
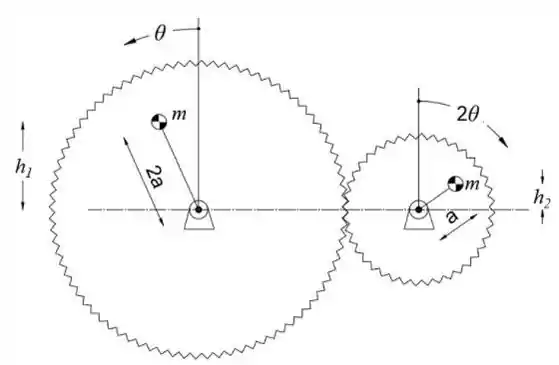
Primeiro, vamos desenhar o diagrama de força ativa
Observe que não há forças externas agindo nem molas ligadas ao sistema, portanto, podemos escrever a equação de equilíbrio como
(1)
Podemos ver no esboço que as alturas h1 e h2 são
Passo 2
Uma vez que temos duas massas aqui, podemos escrever a expressão para a energia potencial gravitacional como
Podemos substituir h1 por 2acosθ e h2 por acos2θ
Derivamos ambos lados da equação
(2)
Passo 3
A seguir, substituiremos δVg pela expressão (2) na equação de equilíbrio (1)
Podemos dividir os dois lados da equação por -2 amg
substituiremos by
O sistema está em equilíbrio quando
Ou
Passo 4
Observe que o sistema é estável quando a segunda derivada da equação de equilíbrio é maior que zero. e instável quando a segunda derivada é menor que zero
A segunda derivada da equação de equilíbrio é
(3)
Passo 5
Para verificar a estabilidade das posições θ = 0∘, 180 ∘, 120 ∘ ,240 ∘, vamos simplesmente colocar o valor de θ na expressão (3) e verificar se a expressão é positiva ou negativo
Uma vez que a segunda derivada é menor que zero, o sistema é instável
Uma vez que a segunda derivada é menor que zero, o sistema é instável
Uma vez que a segunda derivada é maior que zero, o sistema é estável
Uma vez que a segunda derivada é maior que zero, o sistema é estável