Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 73
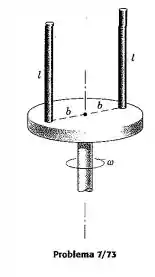
Cada uma das duas hastes de massa está soldada à face do disco que gira em torno do eixo vertical, com uma velocidade angular constante . Determine o momento fletor que atua na base de uma das hastes.
Passo 1
Para resolvermos o problema vamos utilizar as relações de momento fletor e de momento de inércia para calcular qual a sua quantidade total
Passo 2
Temos que todo o sistema gira em tordo do eixo do sistema geral. Para a barra que está soldada no disco, o seu momento fletor irá apontar apenas na direção . Assim, temos que o mesmo será
Como não temos a variação de na direção , temos que . Assim
Resposta
Exercícios de Livros Relacionados
Os cursores nas extremidades da haste telescópica AB deslizam ao longo dos eixos fixos mostrados. Durante um intervalo de movimento, v A = 125 m m / s e v B = 50 m m / s . Determine a expressão vetori
A ponta do cone do Prob. 7/133 é, na realidade, levemente arredondada, fazendo com que o ponto de contato P com a superfície de suporte esteja ligeiramente fora do eixo de giro, conforme ilustrado aqu
As rodas do avião, a jato estão girando na velocidade angular correspondente a uma velocidade de decolagem de 150km/h. O mecanismo de retração opera com θ aumentando à taxa de 30° por segundo. Calcule
O ventilador elétrico possui uma velocidade constante de 1720r p m no sentido indicado com seu eixo orientado conforme mostrado. Se as componentes x e y da velocidade do ponto A na extremidade da pá s
O cone maciço de massa m , raio da base r , e altura h está girando a uma taxa elevada p em torno do seu próprio eixo e é liberado com seu vértice O apoiando em uma superfície horizontal. O atrito é s