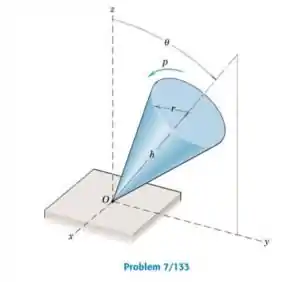
O cone maciço de massa , raio da base , e altura está girando a uma taxa elevada em torno do seu próprio eixo e é liberado com seu vértice O apoiando em uma superfície horizontal. O atrito é suficiente para impedir o vértice de deslizar no plano x-y. Determine o sentido da precessão e o período de uma rotação completa em torno do eixo vertical z.
Passo 1
Bom, para sabermos em qual direção o cone precessiona, vamos calcular o momento para o ponto O e encontrarmos a direção da mudança do momento angular:
O ângulo será o próprio porque a gravidade está na vertical, ou seja, ela forma o mesmo ângulo com o cone que a vertical da coordenada z.
Como a única força que atua no cone é a força gravitacional no seu centro de massa, ficamos com:
Sendo que a posição do centro de massa é:
E é a distância do ponto de atuação da força gravitacional até o ponto O.
A direção do vetor do momento, utilizando a regra da mão direita, será , então:
E por causa disso, o sentido em que ocorre a precessão será no sentido positivo do eixo z, ou seja:
Passo 2
E pela equação de
Sendo k obtido pela Tabela D/4 para os momentos de inercia:
Substituindo o k e a posição do centro de massa do cone sólido:
Passo 3
Por fim, utilizamos a equação do período para uma rotação completa em torno do eixo vertical: