Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 73
A haste de união exerce uma força de na guia como mostrado. Substitua essa força por um sistema força-binário equivalente em .
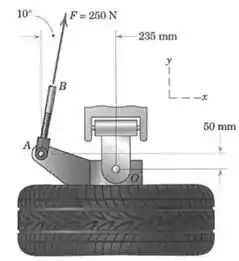
Passo 1
Vamos dividir a força em duas componentes:
E agora queremos calcular o momento de cada uma dessas componentes:
Vamos representar essas duas distâncias no desenho:
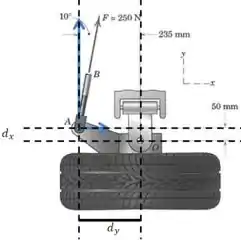
E pelo desenho podemos ver que:
Passo 2
Então beleza, já podemos calcular o módulo do momento total em relação ao ponto :
E esse momento favorece a rotação no sentido horário.
Ótimo, e o outro elemento do nosso sistema força-binário é uma força igual à própria força , mas simplesmente deslocada para ficar sobre o ponto .
Como esse deloscamento não muda em nada a expressão de vamos ter simplesmente:
Resposta
A força deve ser e o binário deve ser no sentido horário.
Exercícios de Livros Relacionados
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta o membro medida a partir de A .
Substitua o carregamento do sistema por uma força e momento de binário resultante equivalente agindo no ponto A .
Substitua o carregamento do sistema por uma força e momento de binário resultante equivalente agindo no ponto A .
Substitua o carregamento do sistema por uma força e momento de binário resultante equivalente agindo no ponto A .
Substitua o carregamento do sistema por uma força e momento de binário resultante equivalente agindo no ponto A .