Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 17

Cada uma das quatro barras móveis uniformes tem uma massa m, e sua posição de equilíbrio na vertical plano é controlado pela força P aplicada ao final da barra inferior. Para um determinado valor de P, determine o ângulo de equilíbrio θ . É possível para o posição de equilíbrio mostrada ser mantida por substituindo a força P por um par M aplicado ao final da barra horizontal inferior?

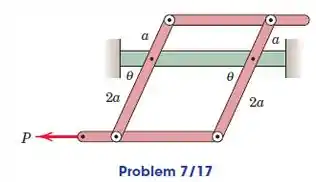
Fonte: Meriam - Estática - 7ª ed

Passo 1

Fala aí gente top!

Vamos com tudo pra mais um probleminha haha!

Primeiro, o problema é bem direto, quer o ângulo θ para o equilíbrio do sistema mostrado.

Depois, quer saber se com a substituição da força P aplicada por um momento M ainda permaneceria o equilíbrio do sistema.

Passo 2

Dito isso, bora fazer nosso diagrama do corpo livre:

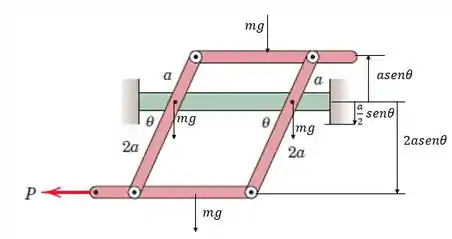
E, aplicando o princípio do trabalho virtual:

δ U = 0 ;                 P δ 2 a c o s θ + m g δ 2 a s e n θ + 2 a 2 s e n θ - a s e n θ = 0                                           ( 1 )

Passo 3

Assim, já podemos reorganizar termos:

δ θ - P a s e n θ + 2 m g a c o s θ = 0

Rearranjando valores, temos:

P s e n θ = m g c o s θ               → θ = tan - 1 ⁡ m g P

Resposta

Portanto

θ = tan - 1 ⁡ m g P

E, se P for substituído por um par de M, nenhum trabalho de M pode ser feito, pois a barra inferior permanece horizontal e não pode girar. Portanto, M não poderia produzir equilíbrio.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força F que a pessoa deve aplicar, tangente ao aro da roda de uma cadeira de rodas, para subir uma rampa inclinada de ângulo θ . A massa combinada da cadeira e da pessoa é m . (Se s é o de
Especifique a força horizontal F necessária para manter o equilíbrio da plataforma de 80 kg em função do ângulo θ feito pelas barras de sustentação em relação à horizontal. Cada uma das três barras un
Ao se testar o projeto mostrado de um macaco guiado por um fuso, 12 voltas na manivela são necessárias para elevar o pedal de 24 mm. Se uma força F = 50 N, aplicada normalmente ao eixo da manivelam é
Calcule a eficiência com a qual a cunha, com inclinação de 5°, eleva o peso W , sob a ação da força horizontal P atuando na cunha. O coeficiente de atrito entre a cunha e o bloco vale 0,30.
A plataforma de trabalho portátil é elevada por intermédio de dois cilindros hidráulicos articulados nos pontos C . Cada cilindro está sob uma pressão hidráulica p e tem uma área de pistão A . Determi