Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 22
Calcule a eficiência com a qual a cunha, com inclinação de 5°, eleva o peso , sob a ação da força horizontal atuando na cunha. O coeficiente de atrito entre a cunha e o bloco vale 0,30.
Passo 1
A eficiência de um mecanismo pode ser calculada pela seguinte relação:
Devemos então calcular o trabalho recebido pela cunha, que é o trabalho da força para um deslocamento da cunha, e o trabalho feito pela cunha para levantar o peso .
Passo 2
Primeiro vamos relacionar a força e o peso , por meio das equações de equilíbrio da cunha. Temos atuando nela a força , a força feita pelo bloco e a força normal feita pelo chão. A força deve ter uma inclinação em relação à normal à superfície igual ao ângulo de atrito .
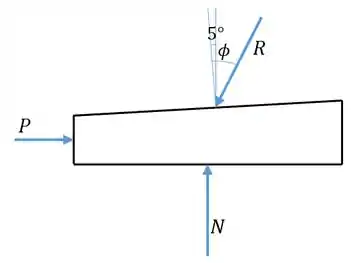
Encontramos o ângulo da seguinte maneira:
Sabemos que a componente vertical de deve ser igual a . O ângulo entre e a vertical é , então:
Pelo equilíbrio horizontal de forças, achamos então a relação entre e :
Passo 3
Agora vamos calcular o trabalho recebido pela cunha e realizado por ela. Se deslocamos a cunha para a direita de uma distância , o bloco de peso irá ser deslocado para cima de uma altura . A razão entre essas dias distâncias é a inclinação da cunha:
O trabalho recebido pela cunha pela força é:
O trabalho realizado pela cunha é:
Então: