Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 20

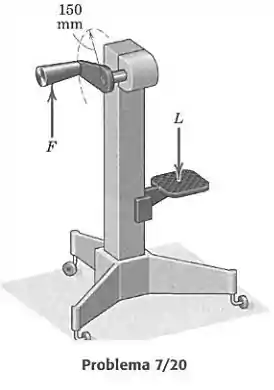
Ao se testar o projeto mostrado de um macaco guiado por um fuso, 12 voltas na manivela são necessárias para elevar o pedal de 24 mm. Se uma força N, aplicada normalmente ao eixo da manivelam é necessária para elevar uma massa de 1,5 Mg, determine a eficiência do fuso ao elevar a carga.

Passo 1

A eficiência de uma máquina pode ser calculada pela seguinte relação:

Devemos então calcular o trabalho recebido pelo macaco, que é o trabalho realizado pelo momento na manivela, e o trabalho feito pela máquina para levantar a massa de 1,5 Mg.

Passo 2

O trabalho feito pelo momento constante para o giro total de ângulo é:

O momento é igual à força de 50 N vezes o raio de 0,15 m:

é o ângulo de 12 voltas:

Então:

Passo 3

O módulo do trabalho feito pela máquina para levantar a massa é o peso da massa vezes a altura de 0,024 m:

Passo 4

Então a eficiência é:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o valor de equilíbrio de x para a barra sustentada por molas. A mola tem uma rigidez ke não é esticada quando x = 0. A força F atua na direção da barra, e a massa da barra é desprezível.

Para o mecanismo mostrado, a mola é descomprimida quando θ = 0. Determine o ângulo θ para a posição de equilíbrio e especifique a rigidez mínima da mola k que limitará θ a 〖30〗 ^ ∘. A haste DE passa l

A energia potencial de um sistema mecânico é dada porV = 6 x 4 - 3 x 2 + 5 , onde x é a coordenada de posição que define a configuração do sistema de um único grau de liberdade. Determine os valores d

Determine a força Q na mandíbula do cisalhamento para a força 400-N aplicada com θ = 30 ∘. (Dica: substitua a força 400-N por uma força e um par no centro da engrenagem pequena. O deslocamento angular

O pequeno cilindro de massa me raio r está confinado a rolar na superfície circular do raio R. Pelos métodos deste artigo, prove que o cilindro é instável no caso (a) e estável no caso (b).