Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 5
- Cada uma das quatro conexões uniformes tem uma massa . Determine a força horizontal , necessária para mantê-las em posição no plano vertical, como mostrado.
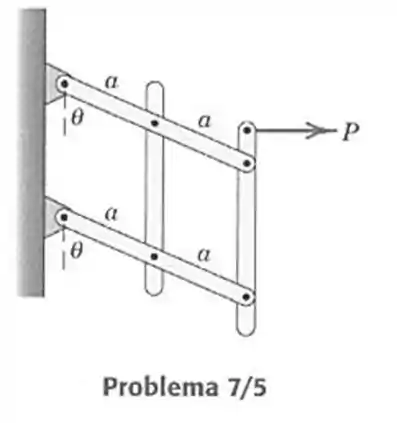
Passo 1
Vamos desenhar as forças presentes no sistema. (Fora de escala)
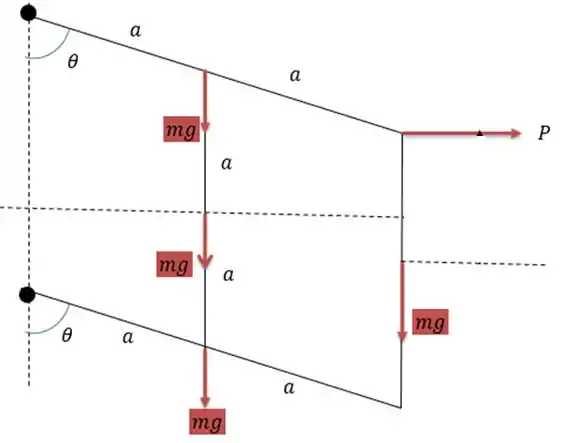
Agora as distâncias presentes no sistema. (Com um pouquinho de escala)
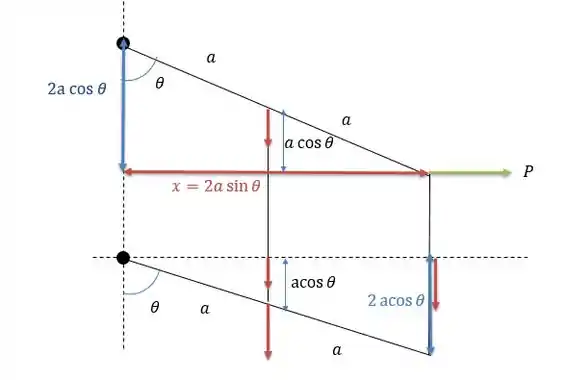
Passo 2
Onde todas as forças tendem a esticar suas linhas, o que nos dá a seguinte equação de somas de trabalhos virtuais:
O que dá:
Isolando :
Resposta
Exercícios de Livros Relacionados
A placa de ventilação é apoiada em B por um pino. Se ela pesa 75N e tem um centro de gravidade em G , determine a rigidez k da mola de modo que a placa permaneça em equilíbrio em θ = 30 ° . A mola est
Uma força horizontal W de intensidade de 324 N é aplicada ao mecanismo em C. Desprezando o peso do mecanismo, determine o valor de θ correspondente ao equilíbrio. A constante da mola é k = 3.6k N / m
Duas hastes AC e CE são unidas por um pino em C e por uma mola AE. A constante da mola é 270 N/m, e a mola está indeformada quando θ = 30 ° . Sabendo que l = 250m m e desprezando os pesos das hastes,
Uma força vertical W é aplicada ao mecanismo articulado em B. A constante da mola é k, e a mola está indeformada quando AB e BC são horizontais. Desprezando o peso do mecanismo, deduza uma equação em
Sabendo que a constante da mola CD é k e que a mola está indeformada quando a haste ABC está horizontal, determine o valor de θ correspondente ao equilíbrio para os dados indicados. P = 300N ,l = 400m