Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 3
- Determine o ângulo de equilíbrio, para uma dada força . Despreze a massa das conexões.
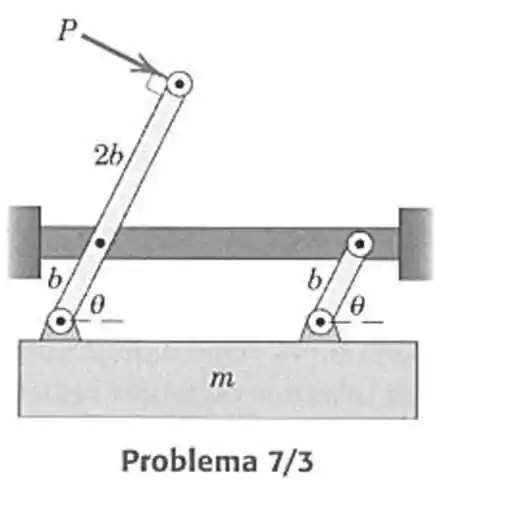
Passo 1
Vamos redesenhar o sistema acima:
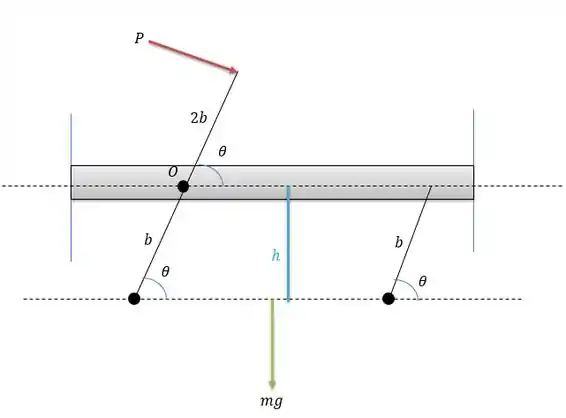
De modo que a força imprime um momento em gerando um trabalho que faz diminuir o ângulo de :
E a peso do bloco de massa faz esticar a linha de modo a termos o trabalho:
De modo que a somatória de trabalhos virtuais nos dá:
Passo 2
A relação entre e existe se fizermos o seno do ângulo abaixo do ponto :
Logo a equação de trabalho virtual do sistema será:
Cortando e isolando o ângulo nós teremos:
Resposta
Exercícios de Livros Relacionados
Sabendo que a constante da mola CD é k e que a mola está deformada quando a haste ABC está horizontal, determine o valor de θ correspondente ao equilíbrio para os dados indicados. P = 300N ,l = 400m m
Determine o valor de θ correspondente para a posição de equilíbrio da haste do problema 10.12, quando l = 750m m , a = 125m m , P = 112N e Q = 180N .
Resolva o Problema 10.30 considerando que a força P é movida para C e atua verticalmente para baixo.
Determine o valor de θ correspondente para a posição de equilíbrio da haste do problema 10.13, quando l = 600m m , a = 100m m , P = 50N e Q = 90N .
Uma barra ABC está ligada aos blocos A e B que podem se mover livremente nas guias mostradas na figura. A constante da mola fixada em A é 3 kN/m, e a mola está indeformada quando a haste é vertical. P