Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 238

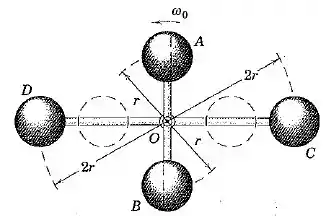
Cada uma das quatro esferas de massa m é tratada como uma partícula. As esferas A e B são montadas em uma haste leve e estão inicialmente girando com uma velocidade angular ω 0 em tordo de um eixo vertical que passa através de O . As esferas C e D também são montadas em uma haste leve que gira independentemente em torno de O e está inicialmente em repouso. O conjunto A B entra em contato com C D onde ranhuras em A e B permitem o acoplamento com C D na posição tracejada indicada. Ambas as unidades em seguida giram com uma velocidade angular comum ω . A resistência por atrito é desprezível. Determine expressões para ω e a percentagem de perda n de energia cinética.

Passo 1

Bom galera, nesse exercício queremos determinar ω e a percentagem de perda de energia cinética. Para o sistema, sabemos que

∑ M 0 = H O ˙ = 0

Dessa forma, o momento angular se conserva.

Passo 2

Como o momento angular se conserva, podemos escrever H O 1 = H O 2

Substituindo a definição que diz H O = m r v = m r 2 ω , temos

2 m r 2 ω 0 + 0 = 2 m r 2 ω + 2 m 2 r 2 ω

Isolando ω , temos

ω = ω 0 5

Passo 3

Perda de energia: Δ Q = T 1 - T 2

Δ Q pode ser dado por

Δ Q = 2 1 2 m r 2 ω 0 2 - 2 1 2 m r 2 ω 2 + 2 1 2 m 2 r 2 ω 2

Substituindo o valor de ω encontrado, temos

Δ Q = m r 2 ω 0 2 - m r 2 5 ω 0 5 2 + 4 5 m r 2 ω 0 2  

Por definição, n = Δ Q T 1 . Substituindo, temos

n = Δ Q T 1 100 % = 4 5 m r 2 ω 0 2 2 1 2 m r 2 ω 0 2 100 % = 80 %

Resposta

ω = ω 0 5

n = 80 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se uma barra de massa desprezível está sujeita a um momento de binário M = 30 t 2N ⋅ m , e o motor do carro fornece uma força de tração F = 15 t N às rodas, onde t está em segundos, determine a veloci
Cada uma das duas esferas tem massa de 3k g e estão fixas a uma barra de massa desprezível. Determine o tempo durante o qual o torque M = 8 t N ⋅ m , onde t está em segundos, deve ser aplicado à barra
A bola B tem massa de 10k g e está fixada à ponta de uma barra cuja massa pode ser desprezada. Se o eixo é submetido a um torque M = 2 t 2 + 4 N ⋅ m , onde t está em segundos, determine a velocidade d
Cada uma das esferas A e B têm massa de 2k g , e estão soldadas às barras leves que estão rigidamente conectadas a um eixo como mostrado. Se o eixo é submetido a um momento de binário M = 1,5 4 t 2 +
O bloco de 5k g repousa sobre uma superfície para a qual μ k = 0,5 . Sobre ele age uma força radial de 10N e uma força horizontal de 35N , sempre direcionada a 30 ° da tangente à trajetória como mostr