Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 92
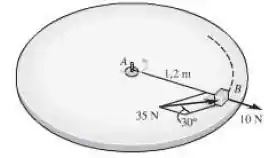
O bloco de repousa sobre uma superfície para a qual . Sobre ele age uma força radial de e uma força horizontal de , sempre direcionada a da tangente à trajetória como mostrado. Se o bloco está inicialmente movendo-se em trajetória circular com a velocidade no instante em que as forças são aplicadas, determine o tempo necessário antes que a tração na corda torne-se . Despreze para o cáculo a dimensão do bloco.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiro vamos descobrir a velocidade a partir do somatório de forças na direção normal. Temos:
Agora que sabemos a velocidade final, vamos aplicar o princípio do impulso e quantidade de movimento angular para descobrir o tempo:
Resposta
Exercícios de Livros Relacionados
O membro ABC tem uma massa de 2,4 kg e está preso a um suporte de pino em B. Uma esfera D de 800 g atinge a extremidade do membro ABC com uma velocidade vertical v1 de 3 m / s. Sabendo que L = 750 mm
Um caixote quadrado uniformemente carregado é liberado do repouso com seu canto D diretamente acima de A; ele gira em torno de A até que seu canto B bata no chão, quando então passa a girar em torno d
Cada uma das barras AB e BC tem comprimento L = 15 pol. e peso W= 2,5 lb. Determine a velocidade angular de cada barra imediatamente após o impulso Q Δ t = ( 0.30 l b ⋅ s ) i i ser aplicado em C.
Em um jogo de sinuca, a bola A está rolando sem escorregar com uma velocidade Vo ao atingir obliquamente a bola B, que está em repouso. Denotando por r o raio de cada bola e por μ k o coeficiente de a
As barras uniformes AB e AC, cada uma com massa m e comprimento l, são parafusadas juntas em A e conectadas por pinos em pequenos roletes em B e C. Uma mola de constante k é presa aos pinos em B e C e