Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 108
Uma força vertical no pedal do dispositivo é necessária para produzir uma força trativa de na barra de controle vertical. Determine as reações correspondentes nos mancais em e .
Passo 1
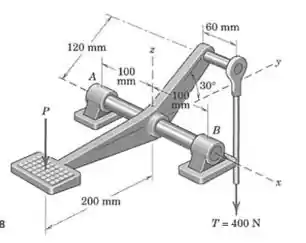
Nosso objetivo é encontrar as forças em e , que pela terceira lei de Newton aponta na direção do eixo na figura, então vamos chamá-las de e .
Além dessas forças nós temos e , que estão representados na figura.
Vamos então procurar algumas equações de equilíbrio que nos ajudem a encontrar essas forças. Começamos com o momento em relação ao eixo , porque nesse caso excluímos as forças e , já que elas cruzam o eixo.
Pelo desenho conseguimos ver que está a do eixo , e está a uma distância dada por . Além disso, as duas forças favorecem a rotação em sentidos diferentes:
Passo 2
Agora ficamos com duas variáveis desconhecidas ( e ), e duas conhecidas ( e ). Vamos escolher um novo eixo de forma que uma das variáveis desconhecidas suma da equação.
A melhor forma de fazer isso é colocar a origem do nosso sistema de coordenadas sobre o ponto , e então calcular o momento em relação ao novo eixo .
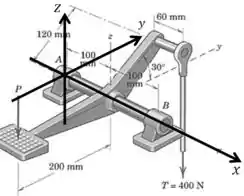
Nesse caso a força tem momento nulo, a força está a do eixo, a força está a e a está a . Depois é só ajustar o sinais:
Passo 3
Agora ficamos apenas com uma variável desconhecida, e por isso podemos usar uma equação mais simples para encontrá-la:
Vamos somar todas as forças na direção do eixo :
E como e só tem componentes na direção , esses já são os módulos das forças nos mancais.
Resposta
As forças são e .