Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 1
Uma caixa de 750 kg é puxada ao longo do solo com uma velocidade constante por uma distância de 7,5 m, utilizando um cabo que forma um ângulo de com a horizontal. Determine a reação no cabo e o trabalho realizado por esta força. O coeficiente de atrito cinético entre o solo e a caixa é .
Passo 1
O enunciado nos deus as seguintes informações:
Massa da caixa: ;
Espaço percorrido:
Ângulo do cabo com a horizontal: ;
Coeficiente de atrito cinético: .
Devemos determinar a reação no cabo e o trabalho realizado por esta força.
Primeiramente, devemos estabelecer nosso sistema de coordenadas inercial e contruir o diagrama de corpo livre da caixa, levando em consideração todas as forças que realizam trabalho no corpo à medida que ele se desloca ao longo de sua trajetória.
Como a velocidade é constante,
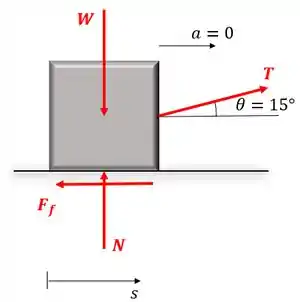
Onde é a força peso, é a força normal, é a força de atrito e é a força exercidade pelo cabo, que puxa a caixa no sentido do deslocamento .
Utilizaremos .
Passo 2
Em seguida, aplicaremos a Equação de Movimento para descobrir o valor de .
Em :
Em :
Substituindo na equação acima, obtemos
Passo 3
Para descobrir o trabalho realizado por , aplicaremos o princípio do trabalho e energia.
Uma força realiza trabalho quando ela se move através de um deslocamento na direção da força. O deslocamento ocorre somente na horizontal e, nesta direção, temos somente a componente , logo