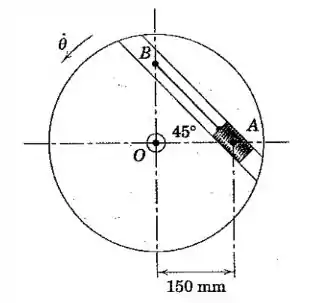
O cursor de se encaixa com folga na ranhura lisa de no disco, que gira em um plano horizontal em torno do seu centro . Se é mantido em posição por um cordão fixo no ponto , determine a tração no cordão para uma velocidade rotacional constante . A direção da velocidade faria alguma diferença?

Para calcular qual é essa aceleração centrípeta, primeiro precisamos converter a velocidade angular para radianos por segundo:

E então a aceleração centrípeta é:

Ok, mas o que isso tem a ver com o cordão? Bom, é ele quem vai fornecer parte da aceleração centrípeta (as paredes do disco também cumprem um papel).

Vamos aplicar a segunda lei de Newton sobre a linha pontilhada na figura:

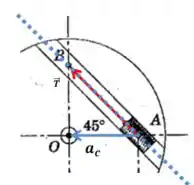
A soma das forças na direção dessa linha é igual a componente da aceleração na direção dessa linha, ou seja:

Agora falta avaliar se uma mudança na direção da rotação geraria uma diferença nesse resultado.

Bom, vamos olhar de novo para a fórmula que nós usamos:

Mudar a direção da rotação é a mesma coisa que trocar o sinal do , mas como ele está elevado ao quadrado, sabemos que o sinal vai “sumir”!

Fisicamente, isso é compreensível, porque mudar a direção do movimento nesse caso é como ver o movimento através de um espelho: os valores não deveriam mudar.