Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 76

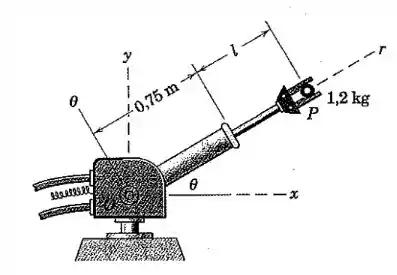
O braço robótico está se elevando e prolongando simultaneamente. Em um determinado instante, θ = 30 ° , θ ˙ = 40   g r a u s / s , θ ¨ = 120   g r a u s / s ² , l = 0,5   m , l ˙ = 0,4   m / s e l ¨ = - 0,3   m / s ² . Calcule as forças radial e transversal F r e F θ que o braço deve exercer sobre a peça segurada P , a qual possui uma massa de 1,2   k g . Compare com o caso de equilíbrio estático na mesma posição.

Passo 1

Ok, o braço robótico vai exercer forças nas direções radial e tangencial. Para sustentar o movimento descrito no enunciado, essas forças precisam atender às seguintes condições:

∑ F r a d = m a r

∑ F t a n = m a θ

E podemos completar essas duas equações com as fórmulas das acelerações em coordenadas polares:

∑ F r a d = m ( r ¨ - r θ ˙ 2 )

∑ F t a n = m ( r θ ¨ + 2 r ˙ θ ˙ )

Passo 2

Agora vamos analisar quais são as forças que atuam em cada direção. Na radial, nós temos a força feita pelo braço e a componente do peso nessa direção:

∑ F r a d = F r - m g sen ⁡ θ

∑ F t a n = F θ - m g cos ⁡ θ

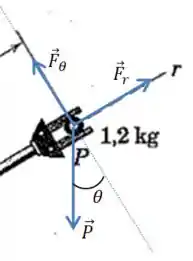
E juntando isso com as equações de cima:

F r - m g sen ⁡ θ = m ( r ¨ - r θ ˙ 2 )

F θ - m g cos ⁡ θ = m ( r θ ¨ + 2 r ˙ θ ˙ )

Passo 3

E agora podemos substituir os valores numéricos em cada caso para encontrar as forças:

F r - ( 1,2 ) ( 9,81 ) ( sen ⁡ 30 ° ) = 1,2 - 0,3 - 1,25 40 π 180 2

F r = 4,79   N

E:

F θ - ( 1,2 ) ( 9,81 ) ( cos ⁡ 30 ° ) = 1,2 1,25 120 π 180 + 2 0,4 40 π 180

F θ = 14,0   N

Perceba que r = 0,75 + l = 0,75 + 0,5 = 1,25   m .

Passo 4

E no caso de equilíbrio estático na mesma posição as acelerações são nulas:

F r - m g sen ⁡ θ = 0

F θ - m g cos ⁡ θ = 0

E então:

F r = 1,2 9,81 sen ⁡ 30 ° = 5,89   N

F θ = 1,2 9,81 cos ⁡ 30 ° = 10,2   N

Pronto!

Resposta

O braço deve exercer as forças F r = 4,47   N e F θ = 14,0   N . E no caso estático precisamos de F r = 5,89   N e F θ = 10,2   N .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as condições indicadas no Prob. 3 / 89 , determine as componentes inerciais x e y da força horizontal P → exercida sobre o cursor pelo tubo imediatamente antes do cursor sair do tubo. Imgem do Pr
O carro de 1500k g está viajando a 100k m / h sobre a porção reta da estrada, e então sua velocidade é reduzida uniformemente de A para C , posição em que este atinge o repouso. Calcule o módulo F da
A atração de parque de diversões consiste em um suporte fixo junto a O , do braço 6mO A , que gira em torno do eixo em O , e do compartimento, que permanece horizontal por meio de um mecanismo em A (n
Quando uma correia em V aciona uma polia em alta velocidade, a ação centrífuga tende a diminuir o seu contato com a polia e consequentemente reduzir a capacidade de transmitir torque. Um dispositivo p
Um pequeno veículo entra no topo A da trajetória circular com uma velocidade horizontal v 0 e ganha velocidade conforme se desloca pra baixo na trajetória. Determine uma expressão para o ângulo β que