Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 78
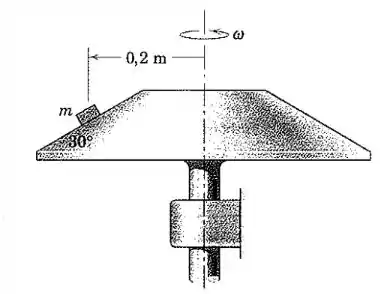
O pequeno objeto de massa é colocado sobre a superfície cônica giratória no raio mostrado. Se o coeficiente de atrito estático entre o objeto e a superfície rotativa é , calcule a máxima velocidade angular do cone em torno do eixo vertical para a qual o objeto não deslizará. Suponha uma variação da velocidade angular muito gradual.
Passo 1
Como a variação da velocidade angular é muito gradual, podemos desprezar os efeitos da aceleração angular.
Vamos desenhar as forças que atuam sobre o bloco:
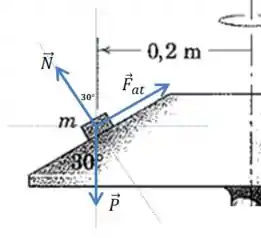
Para atender às condições do enunciado precisamos das seguintes igualdades:
Onde é a direção vertical e é a horizonal, que contém o centro da trajetória circular.
Então beleza, vamos desenvolver nossa solução a partir dessas equações.
Passo 2
As forças na direção vertical são:
E na direção horizontal:
E podemos reescrever a força de atrito como:
Então nosso sistema de equações vira:
Para resolver nosso sistema, têm várias formas, vou dividir a segunda equação pela primeira, pois assim fica mais fácil colocar a nossa velocidade angular () em evidência e vamos poder cortar os termos e .
Vamos ficar então com o seguinte, dividindo ) por ):
E agora é só substituir os valores numéricos:
Resolvido!
Resposta
A velocidade angular máxima do cone é .