Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 20
Pacotes tendo massa de 7,5 kg são transferidos horizontalmente de um transportador para o próximo utilizando uma rampa para a qual . O transportador de cima está se deslocando a 1,8 m/s e os pacotes estão espaçados 0,9 m uns dos outros. Determine a velocidade exigida do transportador de baixo de maneira que nenhum deslizamento ocorra quando os pacotes entram em contato horizontalmente com ele. Qual é o espaçamento entre os pacotes no transportador de baixo?
Passo 1
O enunciado nos dá as seguintes informações:
Massa dos pacotes: ;
Coeficiente de atrito: ;
Velocidade do transportador superior: m/s;
Espaçamento inicial entres os pacotes: m
Devemos determinar a velocidade do transportador inferior de maneira que nenhum deslizamento ocorra quando os pacotes entrarem em contato com ele. Além disso, devemos determinar o espaçamento final entres pacotes.
Vamos desenhar o diagrama de corpo livre de uma caixa qualquer:
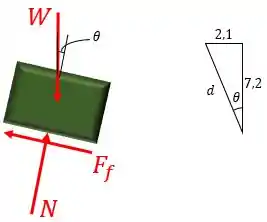
Onde é a força peso, é a força normal e é a força de atrito.
O comprimento pode ser encontrado através de
Passo 2
Vamos começar utilizando as Equações do Movimento.
Em :
Passo 3
Em seguida, aplicaremos o Princípio do Trabalho e Energia.
Durante a descida na rampa, somente a força e a componente realizam trabalho sobre a caixa. O trabalho exercico pela força será negativo, pois o sentido da força é oposto ao deslocamento.
Temos que
onde
Substituindo esses valores na equação inicial, obtemos
Passo 4
Sabemos que
Em , temos que
Portanto, a distância nos pacotes no transportador inferior será