Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 12

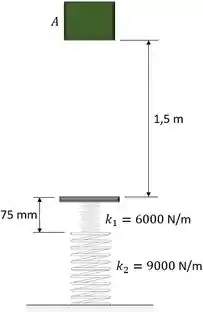
O bloco de 5 kg é solto do repouso em A . Determine a compressão de cada uma das molas após o bloco atingir a plataforma e ser levado instantaneamente ao repouso. Inicialmente, ambas as molas não estão deformadas. Suponha que a plataforma tenha massa desprezível.

Passo 1

O enuncia nos informa que:

Massa do bloco: m = 5   k g ;

Rigidez da mola superior (1): k 1 = 6000   N / m ;

Rigidez da mola inferior (2): k 2 = 9000   N / m .

Incialmente, o bloco está em repouso, portanto sua velocidade inicial v 1 = 0   m / s . Além disso, as molas não estão deformadas.

No segundo momento, após atingir a plataforma, o bloco é levado instantaneamente ao repouso, portanto sua velocidade final será v 2 = 0   m / s . Neste momento, as molas estão comprimidas.

Devemos determinar a compressão de cada uma das molas.

Para visualizar melhor a situação, desenhamos o diagrama de corpo livre do bloco:

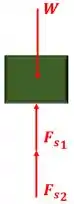
Onde W = m g é a força peso e F s 1 e F s 2 são as forças exercidas pelas molas (1) e (2), respectivamente.

Passo 2

Sabemos que a força elástica é dada como

F s = k s

Onde s é o comprimento da mola deformado.

Precisamos encontrar o valor de s para as molas (1) e (2).

Quando o bloco toca a plataforma e chega ao repouso, a mola (1) terá uma deformação de

s 1 = y

E a mola (2) terá uma deformação de

s 2 = y - 0,075

Onde 0,075 m é o comprimento não deformado da mola (1).

Passo 3

Agora vamos aplicar o Princípio do Trabalho e Energia.

Na direção do movimento do bloco, temos a ação das três forças desenhadas no diagrama de corpo livre. A força peso possui o mesmo sentido do deslocamento, portanto o seu trabalho será positivo. As forças elásticas possuem sentido contrário, logo, o trabalho realizado por elas será negativo.

Além disso, vemos que o bloco cai de uma altura h = 1,5 + y .

Aplicando o princípio, temos que

T 1 + ∑ U 1 - 2 = T 2

Onde

T 1 = 1 2 m v 1 2 = 1 2 m 0 = 0

T 2 = 1 2 m v 2 2 = 1 2 m 0 = 0

U 1 - 2 = W h - 1 2 k 1 s 1 2 - 1 2 k 2 s 2 2

Substituindo esses valores na equação princiapal, obtemos

0 + W h - 1 2 m k 1 2 - 1 2 m k 2 2 = 0

5 ( 9,81 ) 1,5 + y - 1 2 6000 y 2 - 1 2 9000 y - 0,075 2 = 0

y 2 - 9,885 y - 14,712 = 0

Ao resolver a equação de segundo grau, obtemos

y = 0,142   m

Logo,

s 1 = 0,142   m

s 2 = 0,142 - 0,075 = 0,067   m

Resposta

s 1 = 0,142   m

s 2 = 0,067   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a pista deve ser projetada de maneira que os passageiros do carro da montanha-russa não sintam uma força normal igual a zero ou mais do que 4 vezes o seu peso, determine as altura limitantes h A e
A roda de 80 kg tem um raio de giração em relação a seu centro de massa O, ko = 400 mm. Determine a velocidade angular após haver completado 20 revoluções, partindo do repouso.
A roda de 50 kg é submetida a uma forca d 50 N. Se a roda parte do repouso e rola sem deslizar, determine sua velocidade angular depois de haver completado 10 revoluções. O raio de giração da roda em
A barra fina uniforme de 25 kg é submetida a um momento de binário M = 150 N.m. Se a barra está em repouso quando θ = 0 ° , determine a velocidade angular quando θ = 90 ° .
A barra fina uniforme de 50 kg está em repouso na posição mostrada, quando P= 600N é aplicada. Determine a velocidade angular da barra quando ela atinge a posição vertical.