Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 11
O carro de 2 Mg tem uma velocidade quando o motorista vê um obstáculo na frente do carro. Leva 0,75 s para ele reagir e travar os freios completamente, fazendo com que o carro derrape. Se o carro para após ter se deslocado uma distância de 175 m, determine o coeficiente de atrito cinético entre os pneus e a estrada.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do carro: ;
Velocidade inicial do carro: ;
Tempo de frenagem:
Distância percorrida: .
Devemos determinar o coeficiente de atrito cinético entre os pneus e a estrada.
Para conseguir visualizar melhor a situação, desenhamos o diagrama de corpo livre do carro:
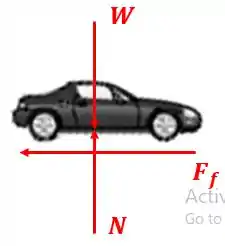
Onde é a força peso, é a força normal e é a força de atrito com o solo.
Passo 2
Primeiramente, vamos encontrar o valor das forças atuantes no carro.
Em :
Como , temos que
Passo 3
Agora utilizaremos o Princípio do Trabalho e Energia para encontrar a distância percorrida pelo carro.
Na direção da trajetória percorrida pelo carro, somente temos a ação da força e que atua no sentido oposto ao deslocamento. Portanto somente ela realizará trabalho sobre o carro, porém com valor negativo.
Aplicando o princípio, temos que
Logo,
Substituindo os valores na equação principal, obtemos
Onde é a distância percorrida após os freio estarem ativados. Lembre-se de que o mtorista demorou 0,75 segundos para reagir e ativar os freios. Portanto, não é a distância total percorrida.
Passo 4
Sabemos que é a distância percorrida pelo carro após os freios estarem ativados e que o motorista demorou 0,75 segundos para reagir e pisar no freio. Durante esse tempo, ele percorreu uma distância .
Portanto, a distância final percorrida será a .
Vamos encontrar o valor de :
Sabemos que
Logo,
A distância total percorrida pelo carro será
Colocando em evidência, obtemos