Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 55
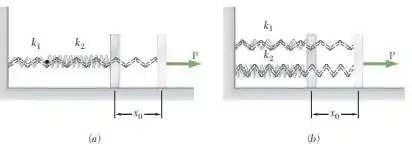
Uma força é lentamente aplicada a uma placa que está presa a duas molas, causando uma deflexão . Para cada um dos casos mostrados na figura, deduza uma expressão para constante , em termos e , de uma mola única equivalente para o sistema dado, isto é, da mola única que sofrerá a mesma deflexão quando submetida à mesma força .
Passo 1
Vamos lá! Queremos calcular a mola equivalente de dois sistemas. Na letra a), as molas estão em série. Já na letra b), as molas estão em paralelo.
Como a influência destes sistemas são diferentes, vamos trabalhar com cada caso separadamente, começando pelo sistema em série.
Aqui, sabemos que a força aplicada nas duas molas são iguais. Portanto, como as molas são lineares, temos:
Somando as duas deformações das molas teremos a deflexão, a qual é . Portanto,
Para finalizarmos, queremos encontrar uma única mola equivalente que, quando submetida a uma força , a sua deformação é . Como esta mola também é linear, temos e consequentemente,
E assim chegamos à relação da mola equivalente em série!
Passo 2
Agora temos a letra b). Aqui, as nossas molas estão em paralelo.
A diferença neste caso é que a deformação de ambas as molas é idêntica, e não as forças! Portanto,
Agora, vamos repetir a análise que fizemos no final do Passo 1. Queremos encontrar uma única mola equivalente que, quando submetida a uma força , a sua deformação é .
Só que quem é esta deformação ? É a soma das outras duas! Portanto,
Por fim, como esta mola também é linear, temos . Logo,
E assim finalizamos a nossa questão!