Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 71
Resolva o problema 14.70 se o coeficiente de atrito cinético entre o plano e acaixa for de
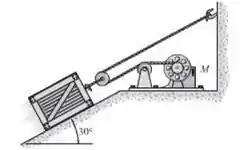
Passo 1
Aplicando a equação de torricelli, teremos
Passo 2
Fazendo o DCL para os eixo a 30° da base e 120°, teremos
N
N
Então a potencia útil utilizada pelo motor será
Resposta
A potência será de 2,28 kW
Exercícios de Livros Relacionados
Uma bola de 1k g em A é suspensa por uma corda inextensível e tem velocidade inicial de 4,8 m / s . Se l = 0,6m e x B = 0 , determine y B de modo que a bola entre no cesto.
Prove que uma força F x , y , z é conservativa se, e somente se, as seguintes relações forem satisfeitas: ∂ F x ∂ y = ∂ F y ∂ x ∂ F y ∂ z = ∂ F z ∂ y ∂ F z ∂ x = ∂ F x ∂ z
A força F = x i + y j + z k x 2 + y 2 + z 2 3 / 2 age sobre uma partícula P x , y , z que se move no espaço. (a) Usando a relação deduzida no Problema 13.79, mostre que essa força é uma força conserva
(a) Calcule o trabalho feito de D a O para a força P do Problema 13.82 por integração ao longo da diagonal do cubo. (b) Usando o resultado obtido na resposta da parte b do Problema 13.82, verifique qu
Uma força F age sobre uma partícula P x , y que se move no plano x y . Determine se a força F é uma força conservativa e calcule o trabalho de F quando P descreve a trajetória no sentido horário A , B