Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 77
Um vagão ferroviário de carvão possui uma massa de vazio transporta uma carga total de de carvão. Os compartimentos são equipados com portas no fundo que permitem o descarregamento do carvão através de uma abertura entre os trilhos. Se o vagão descarrega o carvão na taxa de em sentido descendente em relação ao vagão, e se a resistência por atrito do movimento é por tonelada de massa total restante, determine a força no engate necessária para dar ao vagão uma aceleração de na direção de no instante em que metade do carvão tiver sido desepejada.
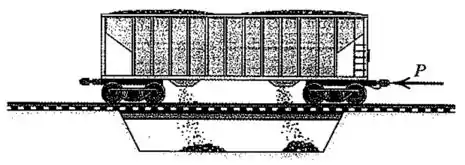
Passo 1
Vamos começar analisando a soma das forças externas na direção horizontal:
Onde é a força de atrito, e é a força no engate. Pelos dados que foram dados no enunciado podemos escrever uma fórmula para o atrito:
E dividimos por porque o atrito aumenta em por tonelada.
Já que a massa do vagão é , e inicialmente tínhamos de carvão, a massa no instante em que metade do carvão já foi despejado é:
E então a força de atrito é:
Passo 2
Ok, então a força externa resultante na direção é:
Sabemos que essa força tem que ser igual à taxa de variação do momento linear na mesma direção:
Onde é a velocidade do fluxo de carvão em relação ao vagão na direção . Como esse fluxo é totalmente vertical, essa velocidade é nula:
A massa já foi calculada no passo anterior:
E queremos fazer nossa conta para o caso em que a aceleração é:
E o sinal negativo aparece por estar na mesma direção da força , que definimos como negativa lá em cima.
Agora podemos substituir tudo na equação:
Resposta
A força necessária é .