Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 70
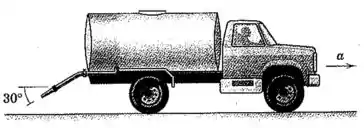
Um caminhão-tanque para lavar as ruas possui uma massa total de quando o seu tanque está cheio. Com o jato igado, de água por segundo escoam do bocal com uma velocidade de em relação ao caminhão no ângulo de mostrado. Se o caminhão está acelerando na taxa de quando inicia em uma estrada horizontal, determine a força de tração necessária entre os pneus e a estrada quando (a) o jato é ligado e (b) o jato é desligado.
Passo 1
(a) Vamos olhar para a soma das forças externas sobre o caminhão na direção :
No caso em que o jato está ligado, a taxa de variação da massa é:
E a única força externa agindo sobre o caminhão é a tração dos pneus que queremos calcular:
Passo 2
(b) E o que muda no caso em que o jato está desligado? A taxa de variação da massa é zero:
E então:
Resposta
(a)
(b)