Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 52
A caixa uniforme de 50 kg repousa sobre a plataforma para a qual o coeficiente de atrito estático é . Se os membros-apoio têm uma velocidade angular rad/s, determine a maior aceleração angular que eles podem ter de maneira que a caixa não deslize ou tombe no instante .
Passo 1
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Primeiramente devemos decompor a velocidade, e consequente aceleração angular fornecida, em suas componentes normal e tangencial da seguinte forma:
Agora, podemos analisar a equivalência do sistema conforme as ilustrações a seguir:
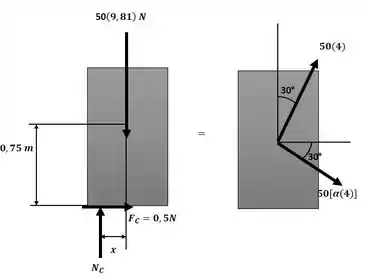
Passo 2
Agora, iremos encontrar todas as equações de movimento do sistema, aplicando somatório de momentos em torno do centro de massa da caixa e o somatório de forças nos eixos x e y:
A distância x representa a posição do ponto C, que é o ponto inferior da caixa onde a mesma está apoiada e cuja localização ainda não é conhecida.
Passo 3
Agora, iremos testar as hipóteses do problema. Começaremos assumindo que a caixa está na condição limite de escorregamento, ou seja:
Substituindo esse valor na primeira equação do passo 2 para encontrar a posição x, obtemos:
O que seria impossível, uma vez que a largura da caixa é de 0,5 m e a distância x é avaliada a partir do centro da mesma, logo, essa condição não é atendida, ou seja, a caixa não desliza.
Sendo assim, analisaremos o caso limite onde a caixa tombaria, logo, o ponto de apoio está justamente em sua extremidade:
Substituindo esse valor na equação 1 do passo 2, temos:
Substituindo esse valor na terceira equação do passo 2, temos:
E, por fim, substituindo o valor encontrado de na segunda equação do passo 2, obtemos: