Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 14

Um carro de corrida tipo dragster parte do repouso e tem uma velcidade descrita pelo gráfico. Construra o gráfico s - t para o intervalo de tempo 0 ≤ t ≤ 15 s. Também, determine a distância total percorrida durante esse intervalo de tempo.

Passo 1

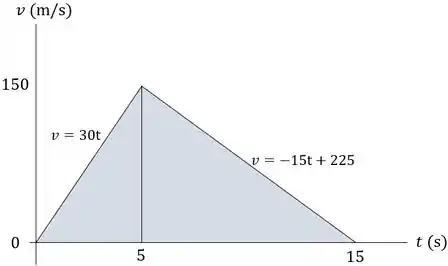
Através do gráfico fornecido, vemos que o carro parte do repouso com uma velocidade v = 30 t por 5 s. A partir de t = 5 s, a velocidade v = - 15 t + 225 vai caindo até se tornar nula em t = 15 s.

Portanto, podemos dividir o trajeto do carro em dois intervalos de tempo. Estes são:

Intervalo 0 ≤ t < 5 :

v 0 = 0

v = 30 t

Intervalo 5 < t ≤ 1 5 :

v = - 15 t + 225

v f = 0

Devemos construir o gráfico s - t para o intervalo de tempo 0 ≤ t ≤ 15 e determinar a distância total percorrida pelo carro.

Passo 2

Sabemos que

v = d s d t

d s = v   d t

Para obter o valor de s , devemos integrar a equação acima utilizando as condições iniciais dadas pela questão.

No intervalo 0 ≤ t < 5 :

v = 30 t

Logo,

∫ 0 s d s = ∫ 0 t 30 t d t

s = 30 t 2 2

No intervalo 5 < t ≤ 15 :

v = - 15 t + 225

s 0 = 30 ( 5 ) 2 2 = 375

Logo,

∫ 375 s d s = ∫ 5 t - 15 t + 225 d t

s - 375 = - 15 t 2 2 + - 15 5 2 2 + 225 t - 225 ( 5 )

s = - 7,5 t 2 + 225 t - 562,5

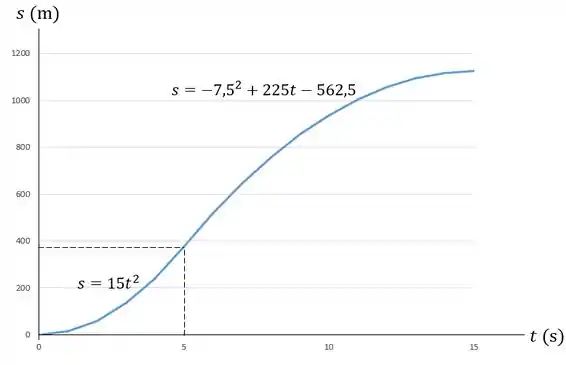
O gráfico ficará da seguinte forma:

Passo 3

Para encontrar a distância total percorrida pelo carro, basta encontrar a área sob o gráfico v - t .

A área do triângulo é igual à

b h 2

Onde b é a base e h   a altura.

Logo,

s = 15 - 0 150 - 0 2

s = 1125   m

Resposta

s = 1125   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O trenó motorizado desloca-se ao longo de um curso reto de acordo com o gráfico v-t. Construa os gráficos s - t e a - t para o mesmo intervalo de tempo de 50 s. Quando t=0 , s=0 .
Um carro parte do repouso e move-se ao longo de uma estrada reta com uma velocidade descrita pelo gráfico. Determine a distância total percorrida até o carro parar. Construa os gráficos s - t e a - t
A posição de um ciclista viajando ao longo de uma estrada reta é descrita pelo gráfico. Construa os gráficos v - t e a - t .
Um carro esportivo move-se ao longo de uma estrada reta com uma aceleração-desaceleração descrita pelo gráfico. Se o carro parte do repouso, determine a distância s’ que o carro se desloca até parar.
A posição de um ciclista viajando ao longo de uma estrada reta é descrita pelo gráfico. Construa os gráficos v - t e a - t .