Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 147
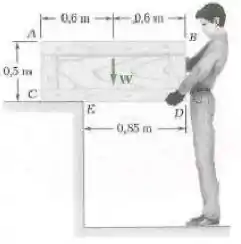
Um caixote de massa é mantido na posição mostrada na figura. Determine o momento produzido pelo peso do caixote em relação ao ponto , a menor força aplicada em que produz um momento de igual intensidade e sentido oposto em relação a .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O momento produzido pelo peso do caixote é calculado multiplicando a magnitude da força pela distância da linha de ação de até o ponto .
Essa distância é dada por:
Portanto:
Passo 2
Item b:
Para que a força aplicada em seja a menor possível e ainda capaz de produzir momento de intensidade em , esta deve ser perpendicular a um segmento de reta que liga os pontos e .
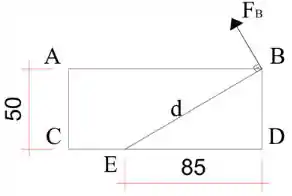
Teremos que:
Portanto:
E para o ângulo:
Resposta
Exercícios de Livros Relacionados
Determine os diagramas de esforço cortante e de momento fletor para a viga em balanço.
Determine os diagramas de esforço cortante e de momento fletor para a viga A B C D E . Todas as polias têm um raio de 0,3m . Despreze o peso da viga e da montagem das polias. A esfera pesa 1,5k N .
Determine os diagramas de esforço cortante e de momento fletor para a viga simplesmente apoiada.
Determine os diagramas de esforço cortante e de momento fletor para a viga simplesmente apoiada.
Determine os diagramas de esforço cortante e de momento fletor para a viga ( a ) em termos de parâmetros mostrados; ( b ) faça M 0 = 500N ⋅ m , L = 8m .