Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 41
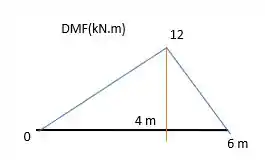
Determine os diagramas de esforço cortante e de momento fletor para a viga simplesmente apoiada.
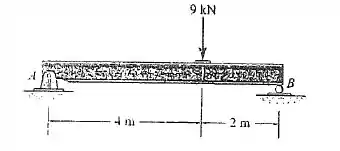
Passo 1
Fala!
O problema quer que a gente encontre o diagrama de esforço cortante e de momento fletor.
Primeira coisa a se fazer é calcular as reações e . Considerando que ambas estão para cima.
Vamos então considerar como eixo de rotação e o sentido horário positivo
Assim, encontramos:
Pelo somatório de forças em :
Ficamos com:
Agora a gente vai encontrar as equações de momento e de cortante para essa viga. Com elas a gente faz o diagrama.
Passo 2
Para isso, vamos começar secçionando a viga em duas regiões: e . Percebe que é a região antes da força concentrada e a depois.
Então vamos pegar cada região e faremos os cálculos das forças e momento, levando em consideração que corpo encontra-se em equilíbrio, isso que dizer que o somatório das forças exercidas sobre ele é .
Vamos olhar para primeira região, fazer um seção genérica a uma distância de Depois vamos posicionar o momento e cortante orientados positivamente nessa seção. Aí achamos as equações pelo equilíbrio.
Olha para a região , já substituindo os valores de e
Pelo equilíbrio:
Então, esse é o esforço cortante nessa região.
E o momento fletor nessa seção localizada em , considerando o sentido anti-horário positivo
Passo 3
E agora, vamos para a região . Vamos cortar nossa viga numa seção genérica nesse intervalo e olhar para a esquerda
O efeito cortante na região é:
E o momento fletor na seção, considerando o sentido anti-horário positivo
Passo 4
Agora que a gente tem as equações para todos os intervalos, nós as plotamos. E assim surge nossos diagramas
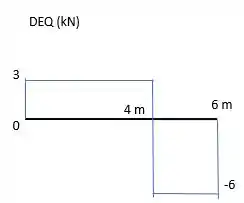
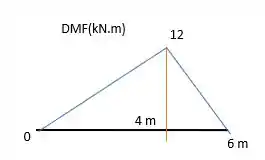
Resposta
