Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 16
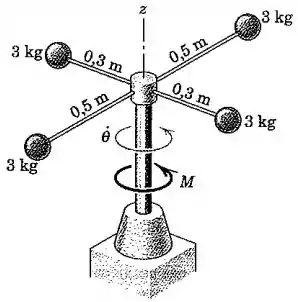
As quatro esferas de estão rigidamente montadas na estrutura e eixo com rotação, que estão inicialmente girando livremente em torno do eixo vertical na velocidade angular de no sentido horário quando visto de cima. Se um torque constante é aplicado ao eixo, calcule o tempo para inverter o sentido da rotação e atingir uma velocidade angular no mesmo sentido de .
Passo 1
Vamos lembrar da seguinte equação:
No nosso caso, o momento resultante é a constante . Então:
Rearranjando os termos, obtemos a seguinte equação diferencial:
Agora, integraremos a equação obtida nos dois lados:
Passo 2
Nesse caso, teremos:
Então:
Substituímos os valores:
Resposta
Exercícios de Livros Relacionados
Se o eixo é submetido a um torque M = 30 e - 0,1 tN . m , onde t é dado em segundos, determine a velocidade angular da montagem qundo t = 5 s, partindo do repouso. A placa retangular tem uma massa de
A estrutura do rolo tem uma massa de 5,5 Mg e um centro de massa em G. O rolo tem uma massa de 2 Mg e um raio de giração em relação a seu centro de massa k A = 0,45m . Se um torque M = 600 N.m é aplic
O disco circular de 25 kg está fixado ao garfo através de um eixo liso A. O parafuso C é usado para travar o disco ao garfo. Se o garfo é submetido a um torque M = 5 t 2N . m , onde t é dado em segund
Por razões de segurança, a perna do apoio de 20 kg de um sinal é projetada para quebrar com uma resistência desprezível em B quando a perna é submetida ao impacto de um carro. Supondo que a perna está
O corpo e a caçamba de uma minicarregadeira têm uma massa de 1000 kg, e seu centro de gravidade está localizado em G. Cada uma das quatro rodas têm uma massa de 50 kg e um raio de giração em relação a