Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 12

Calcule o centroide da área a seguir:

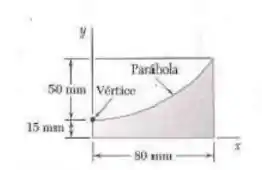
Passo 1

Fala galerinha boa, o problema é de estática mas a gente não pode ficar parado, bora resolver essa aqui.

Nosso objetivo aqui é encontrar o centróide dessa figurinha aí, a gente então pode separar em duas figuras geométricas conhecidas, retângulo e semi-parábola.

Lembrando que o centróide é dado por:

overset(-)(x) = (sum overset(-)(x)_i A_i)/(sum A_i)

E

overset(-)(y) = (sum overset(-)(y)_i A_i)/(sum A_i)

Então vamos ao cálculo dos produtos:

A xx overset(-)(x)_r e t â n g u l o = 40 xx 80 xx 65 = 208000

A xx overset(-)(y)_r e t â n g u l o = 32,5 xx 80 xx 65 = 169000

Já o da semi-parábola será:

Onde

A = (2)/(3) b a s e xx a l t u r a

overset(-)(x)_p a r á b o l a = (2)/(5) b a s e ( C a s o d e s e m i - p a r á b o l a i n v e r t i d a )

E

overset(-)(y)_p a r á b o l a = (5)/(8) a l t u r a ( C a s o d e s e m i - p a r á b o l a i n v e r t i d a )

Assim o cálculo será:

A xx overset(-)(x)_p a r á b o l a = (2)/(5) xx 80 xx (2)/(3) xx 80 xx 50 = 85333,33 m m^3

A xx overset(-)(y)_p a r á b o l a = (15 + (5)/(8) xx 50) xx (2)/(3) xx 80 xx 50 = 123333,33 m m^3

Passo 2

Agora que temos os produtos vamos calcular a área total da figura, que pode ser dada por:

A = A_r e t - A_S e m i P

A_r e t = 65 xx 80 = 5200 m m^2

A_S e m i P = (2)/(3) xx 50 xx 80 = 2666,67 m m^2

Assim a área será:

A = 5200 - 2666,67 = 25 33,33 m m^2

E enfim o cálculo do centróide em x:

overset(-)(x) = (sum overset(-)(x)_i A_i)/(sum A_i)

overset(-)(x) = (208000 - 85333,33)/(25 33,33) = 48,42 m m

E em y:

overset(-)(y) = (sum overset(-)(y)_i A_i)/(sum A_i)

overset(-)(y) = (169000 - 123333,33)/(2533,33) = 18,02 m m

Resposta

overset(-)(x) = 48 , 4 2 m m

overset(-)(y) = 18,02 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a coordenada x do centroide do segmento esférico sólido.
Determine a coordenada z do centroide do volume gerado pela revolução de 180° da área sombreada em torno do eixo z - .
Determine a coordenada x do centro de massa da parte da casca esférica, que tem espessura uniforme, mas fina.
Determine as coordenadas x e y do centroide da área sombreada.
Determine a coordenada x do centro de massa do hemisfério homogêneo, que teve removida a região hemisférica menor.