Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 1.1 - Ex. 12
Calcule a distância a partir do centro do Sol na qual uma partícula experimenta atrações iguais da Terra e do Sol. A partícula está restrita à linha que une os centros da Terra e do Sol. Justifique as duas soluções fisicamente.
Passo 1
Como estamos lidando com três corpos (a partícula, o sol e a Terra), é uma boa ideia definir um referencial:
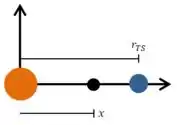
Onde é a distância entre os centros da Terra e do Sol, e é a distância da partícula até o centro do Sol.
E vamos lembrar da fórmula para a força gravitacional:
Passo 2
Escrevendo e igualando as forças entre os pares partícula-Terra e partícula Sol, ficamos com a seguinte equação:
Vamos dividir os dois lados por e reorganizar a equação:
Agora podemos substituir os valores numéricos das massas e distância.
Passo 3
É importante resolver essa equação na calculadora sem arredondar os valores, uma vez que estamos lidando com valores em ordens de grandeza muito variadas, e arredondamentos podem fazer muita diferença.
Aplicando a fórmula de Bháskara na equação quadrática:
E as duas soluções são:
E esses são os possíveis valores para a distância a partir do centro do Sol.
É natural que haja duas soluções, uma vez que a força da gravidade decai com o quadrado da distância. Fisicamente, isso nos diz que uma distância reduzida pode “compensar” as diferenças nas massas do Sol e da Terra, produzindo dois pontos de equilíbrio.
Resposta
As distâncias possíveis são e .