Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 74
74- Calcule, em função de , a energia potencial total para a porta industrial do Prob. 7/69 e verifique o resultado dado para aquele problema. Considere tendo como referência . Observe que a energia potencial da parte da porta cilíndriva é uma constante, que pode ser considerada valendo zero, por conveniência.
Passo 1
Do problema 69 nós encontramos para equação da energia a expressão:
Com valor em Joules e para essa questão , logo:
Passo 2
Plotando o gráfico para indo de 0 até 2.5 teremos:
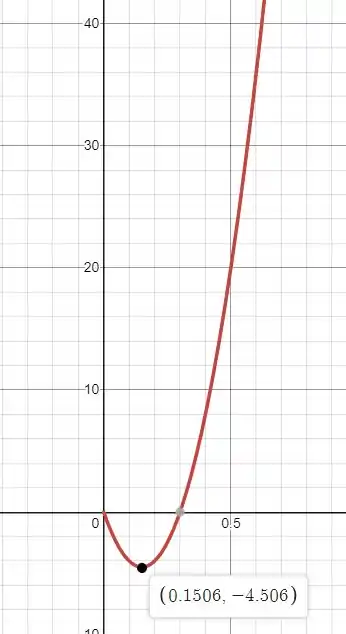
Gráfico de .
Resposta
E gráfico do passo A posição de é mínimo local da função.
Exercícios de Livros Relacionados
As duas hastes possuem massa de 8k g cada. Determine a rigidez k exigida para a mola, de modo que haja equilíbrio quando θ = 60 ° . A mola tem comprimento de 1m quando não deformada. Investigue a esta
Determinar o ângulo θ para haver equilíbrio e investigar a estabilidade nessa posição. As hastes possuem massa de 10k g cada e a mola tem comprimento não deformado de 100m m .
Se cada um dos três elementos do mecanismo tem peso W , determine o ângulo θ de equilíbrio. A mola, que sempre permanece na vertical, não está deformada quando θ = 0 ° .
Uma mola com rigidez à torção k está presa à articulação em B . Ela não está deformada quandoo conjunto de hastes está na posição vertical. Determine o peso W do bloco que resulta em equilíbrio neutro
Se a haste uniforme O A tem massa de 12k g , determine a massa m que a manterá em equilibrio quando θ = 30 ∘ . O ponto C coincide c o m B quando OA está na horizontal. Despreze o tamanho da polia em