Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 34
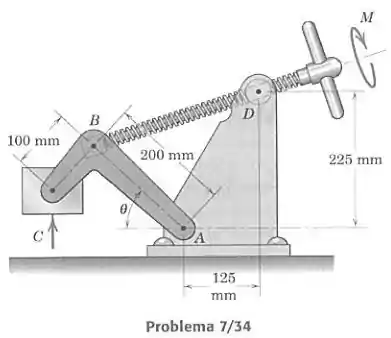
Na morsa acionada por um parafuso, um torque aplicado à manopla do parafuso aperta a morsa aumentando a distância e, portanto, produzindo uma força de aperto . O parafuso é rosqueado através da bucha articulada em , tendo uma rosca quadrada simples com um passo (avanço por revolução) de 4 mm. Considere que não há atrito e expresse a força de aperto , em newtons, em função do torque , medido em newton-metros, para uma posição .
Passo 1
Utilizando o Princípio do Trabalho Virtual, se o sistema está em equilíbrio o trabalho virtual total realizado pelas forças externas ativas (forças que realizam trabalho) para um deslocamento pequeno do sistema deve ser zero:
Os nossos agentes externos ativos são o torque na manopla e a força Devemos calcular calcular então o trabalho virtual realizado pelo momento e pela força, para um giro de angulação do parafuso que causa variação pequena do ângulo . Depois aplicamos o Princípio do Trabalho Virtual, relacionando e .
Passo 2
Primeiro vamos calcular o trabalho realizado pela força . O giro do parafuso aumenta o tamanho de , e isso faz com que a altura do ponto de aplicação de diminua. O trabalho realizado por é dado por
Mas precisamos relacionar com o ângulo , e faremos isso a partir da geometria do desenho:
Olhando o desenho, a altura em função de é:
Derivando essa expressão, temos a variação infinitesimal de :
Então temos o trabalho realizado por :
Podemos substituir por :
Esse valor está em mili-Joules, pois usamos os valores em milímetros. Vamos então fazer uma correção, dividindo por 1000, e aí obtemos o valor do trabalho em Joules:
Passo 3
Agora vamos calcular o trabalho realizado pelo momento na manopla. Se o giro do parafuso e da manopla é de ângulo , no mesmo sentido do momento, então o trabalho é:
Precisamos relacionar com . Primeiro, vamos ver como o giro do parafuso irá aumentar o tamanho de . Vamos planificar uma parte da rosca de uma volta inteira. A circunferência é de , e a variação do comprimento é o passo por revolução. Também representamos a pequena angulação , que possui o tamanho do arco e a variação correspondente do comprimento .
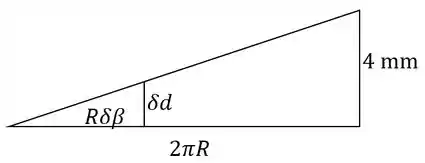
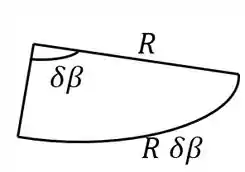
Pela semelhança de triângulos:
deve estar em milímetros para essa expressão de . Agora só falta colocar em função de . Vamos olhar de novo pro desenho:
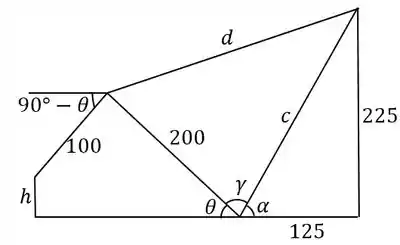
Primeiro vamos encontrar o tamanho e o ângulo fixo . Por pitágoras:
Então o ângulo fica definico em função de :
Derivando, o valor constante desaparece e obtemos:
Agora vamos olhar para o triângulo que tem lados , e 200. Temos 2 lados e 1 ângulo e queremos achar o terceiro lado. Então vamos usar a lei dos cossenos:
Derivando essa expressão, temos:
Trocando por :
Agora calculamos, sabendo que :
Essa expressão dá o valor de em milímetros. Então temos finalmente o valor de em função de :
Passo 4
Pelo Princípio do Trabalho Virtual, temos então:
Cortando :