Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 18

Substituia a força agindo na conexão do Prob. 7/17 por um binário . Determine o momento do binário necessário para manter o equilíbrio em uma posição arbitrária caracterizada pelo ângulo . O momento depende do número de seções existentes?

Passo 1

Substituindo a força do Prob. 7/17 por um momento, temos a seguinte configuração:

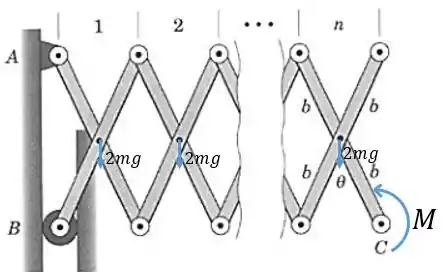
Utilizando o Princípio do Trabalho Virtual, se o sistema está em equilíbrio o trabalho virtual total realizado pelas forças externas ativas para um deslocamento pequeno do sistema deve ser zero:

Os nossos agentes externos ativos (que realizam trabalho em um deslocamento do sistema) são os pesos das barras e o momento atuando no ponto . A força em não pode realizar trabalho, pois esse ponto não se move. A força em também não, pois a força é horizontal e o deslocamento nesse apoio só pode ser vertical. Então devemos relacionar o trabalho infinitesimal causado pelos pesos e pelo momento com , e então igualar o trabalho total a zero.

Passo 2

Primeiro vamos calcular o trabalho virtual causado pelo peso das barras. Para uma variação da distância vertical dos centros das barras em relação ao ponto , temos:

A altura dos centros das barras em relação a é dada por:

Então para um deslocamento , temos, por derivação:

Então o momento realizado pelos pesos é dado por:

O sinal negativo faz sentido, pois se aumentar os centros irão subir, e como a força peso é para baixo o trabalho é negativo.

Passo 3

Agora calculamos o trabalho virtual causado pelo momento. Para um aumento cada barra irá girar um ângulo de no sentido anti-horário, mesmo sentido do momento. Então, temos o trabalho na barra que contém o ponto :