Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 79
Calcule a tensão T necessária para baixar a carga de 800 kg descrita no Prob. 6/78. Encontre também T0.
Passo 1
Primeiro, vamos isolar e desenhar o diagrama de corpo livre do gancho com carga anexada a ele
Peso da carga é
Passo 2
Para que o sistema esteja em equilíbrio, a força de reação R deve ser vertical, portanto, podemos calcular sua magnitude igualando a soma das forças na direção y a zero
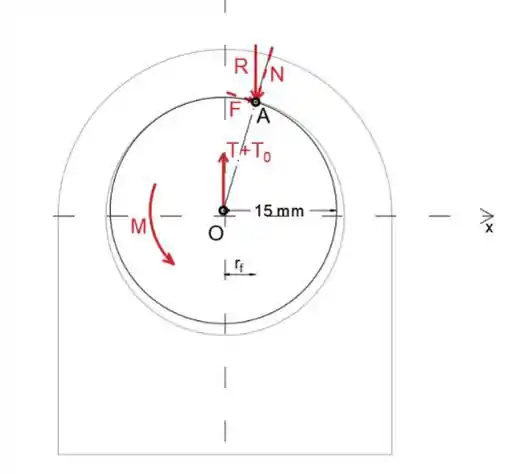
A seguir, substituiremos as forças T e T_0 pela força T + T0 e o par M atuando no ponto O
Observe que, uma vez que estamos tentando diminuir a carga, a força T é menor que T0, portanto, o par M é no sentido anti-horário e sua magnitude é igual ao produto da diferença entre as forças T e T0 e raio de 150 mm
(1)
A seguir, desenharemos o diagrama de corpo livre do eixo
Observe que vamos assumir que o raio do eixo e do rolamento é igual
O ângulo que o R resultante faz com a força de reação normal N é
Uma vez que conhecemos o ângulo ϕ e o raio do eixo, podemos determinar o raio do círculo de atrito rf
Passo 3
Equacionando a soma de foroes na direção y a zero, podemos determinar a soma das tensões T e T0
Ao igualar a soma dos momentos sobre o ponto O a zero, podemos determinar o par M necessário para girar a bobina
Substituiremos M por seu valor na expressão (1) para calcular a diferença nas tensões T e T0
Ao adicionar as expressões (2) e (3), podemos determinar a tensão T
Finalmente, subtraindo as expressões (2) e (3), podemos determinar a tensão T0